この記事ではExcelで「データ分析ツール」を使用したt検定のやり方を具体例を使って紹介します。
【この記事でわかること】
・エクセルを使ったt検定のやり方
・t検定の種類の選び方
エクセルt検定の準備
エクセルでは「データ分析ツール」を使用した方法と、関数を使って計算する方法の2つがありますが、今回は「データ分析ツール」を使う場合です。
エクセルの「データ分析ツール」を使用する方法
Excelには「データ分析」ツールがあり、これを使うと簡単にt検定を実施できます。ただし、このツールはデフォルトでは有効化されていないことが多いので、まずは「データ分析」ツールを有効化する必要があります。
【データ分析ツールの有効化手順】
1. Excelを開き、「ファイル」タブをクリックします。
2.「オプション」を選択します。
3.「アドイン」カテゴリを選択し、「分析ツール」を見つけます。
4.「Excelアドイン」を選択し、「設定」をクリックします。
5.「分析ツール」にチェックを入れ、「OK」をクリックします。
エクセルt検定の種類
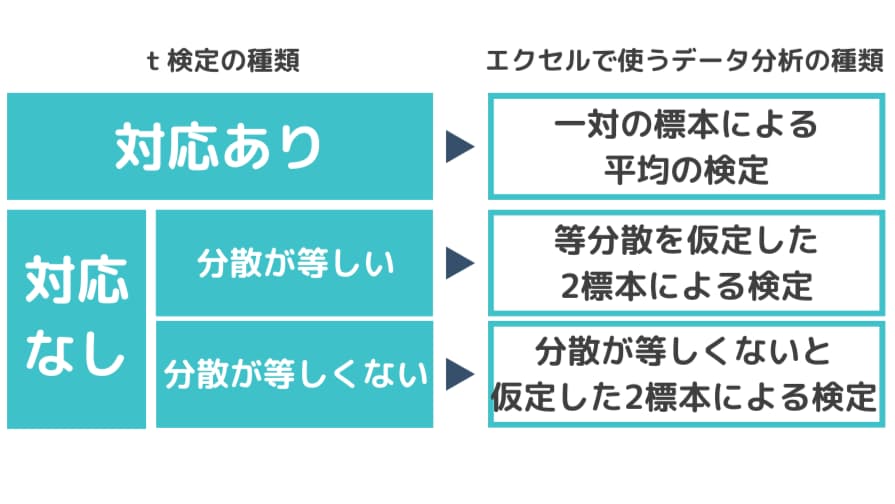
t検定は大きく分けると以下の3種類があり、エクセルの分析ツールでも各t検定に対応した分析方法を選択する必要があります。
- 対応ありのt検定
⇒分析ツール「t 検定:一対の標本による平均の検定」 - 対応なし、分散が等しい
⇒分析ツール「t 検定:等分散を仮定した2標本による検定」 - 対応なし、分散が等しくない(Welch法)
⇒分析ツール「t検定:分散が等しくないと仮定した2標本による検定」
’対応あり’ ’対応なし’とは?
対応あり:関連する2つのグループ(たとえば、同じ被験者の投薬前後の測定値)の平均が異なるかどうかを調べるときに使用します。
対応なし:2つの独立したグループの平均が異なるかどうかを調べるときに使用します。
また、分散が等しいかどうかは、F検定という手法を使って調べます。
具体例でエクセルt検定のやり方を解説
エクセルでのt検定は以下の手順で進めていきます。
【データ分析ツールのt検定手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「t検定」を選択
(例:「t検定:等分散を仮定した2標本間のt検定」)
3.比較するデータ範囲、出力範囲、その他オプションを指定
4.「OK」をクリックしてt検定を実行
では、実際にエクセルを使ったt検定のやり方をt検定の種類ごとに見ていきましょう。
エクセルt検定の具体例①|一対の標本による平均の検定
ある企業で従業員の生産性を向上させるための新しいトレーニングプログラムを導入したとします。トレーニング前後の生産性スコアを比較して、プログラムの効果をt検定で判定してみましょう。
帰無仮説:トレーニングプログラムで生産性は向上しない
対立仮説:トレーニングプログラムは生産性が向上する
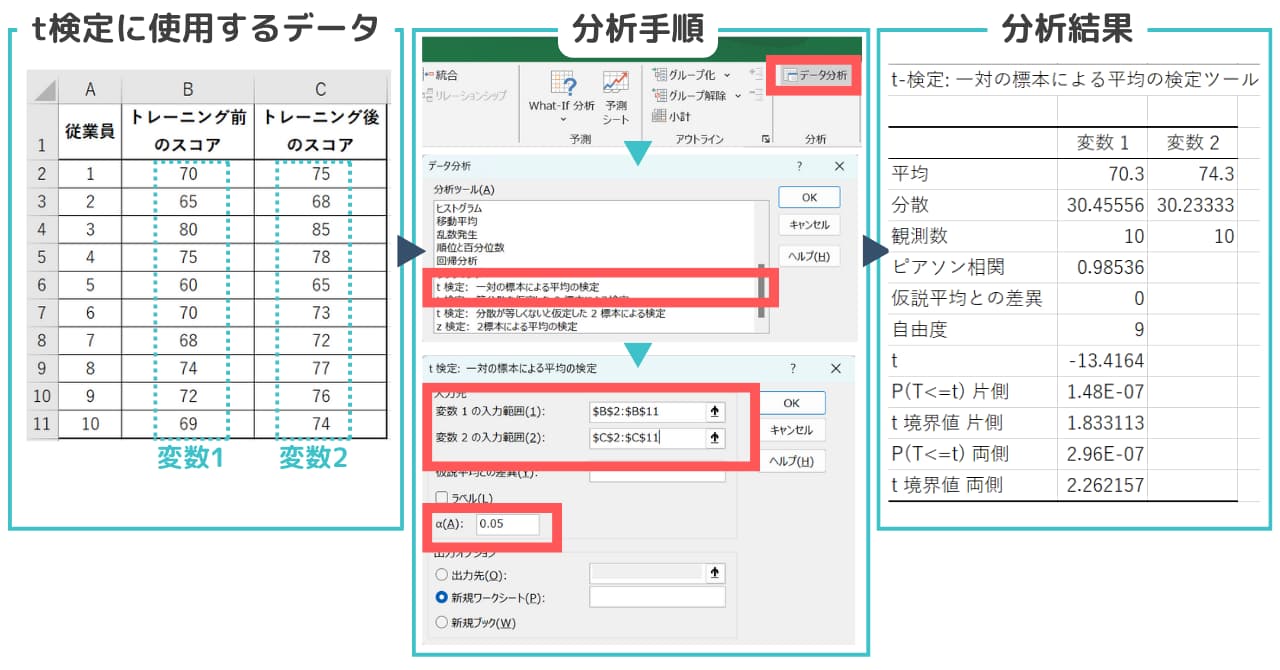
【データ分析ツールを使ったt検定手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「t検定:一対の標本による平均の検定」を選択
3.トレーニング前と後のデータ範囲を選択
4.ラベル(有意水準α)を入力(今回は0.05)
5.「OK」をクリックしてt検定を実行
今回は「向上したかどうか」なので片側検定の値に着目します。結論は、p値(1.48E-7)は非常に小さい値であり、帰無仮説(トレーニングプログラムは従業員の生産性に影響を与えない)を棄却し、統計的に有意な差があると判断できます。つまり、トレーニングプログラムは従業員の生産性に統計的に有意な影響を与えたと言えます。
分析結果項目の説明
- 平均:各データセットの平均値。
- 分散:各データセットの不偏分散。不偏分散とはサンプルデータの分散を計算する際に母集団の分散を推定するためのものです。
- 観測数:各データセットのサンプルサイズ。すなわち、各データセットのデータ点の数です。
- ピアソン相関:2つのデータセット間のピアソン積率相関係数。この値は、データセット間の線形関係の強さと方向を示します。
- 仮説平均との差異:t検定において仮定する平均値の差異。この値がゼロの場合、2つのデータセットの平均値が等しいことを仮定します。
- 自由度:サンプルサイズから1を引いた値。自由度はデータのばらつき具合を考慮するための指標です。
- t値:データから算出されたt値。この値は2つのデータセット間の平均値の差異が統計的に有意であるかどうかを判断するために使用します。
- P(T<=t)片側:片側検定の場合のP値。片側検定は、特定の方向(例:平均値が大きいまたは小さい)における有意性を検定します。
- t境界値 片側:片側検定の場合の棄却限界値。この値をt値が超えると、帰無仮説を棄却し、差異が統計的に有意であると判断します。
- P(T<=t)両側:両側検定の場合のP値。両側検定は、どちらの方向にも偏りがない場合の有意性を検定します。
- t境界値 両側:両側検定の場合の棄却限界値。この値をt値が超えると、帰無仮説を棄却し、差異が統計的に有意であると判断します。
≫Excel関数を使って「対応のある2標本のt検定」を手動で計算するやり方
≫対応のあるt検定を例題で詳しく解説
エクセルt検定の具体例②|等分散を仮定した2標本による検定
ある学校で実施された新しい教育プログラムの効果を評価するためのデータとして、2つのクラス(クラスAとクラスB)のテストスコアを使ってt検定をやってみましょう。
クラスAとクラスBのテストスコアは、互いに独立した2つのサンプル群からのものであり、同じ生徒の前後のスコアを比較しているわけではありません。したがって、ここでは「2標本対応なしのt検定(等分散を仮定した2標本による検定)」を選択するのが適切です。
帰無仮説:クラスAとクラスBの平均スコアに差がない
対立仮説:クラスAとクラスBの平均スコアに差がある
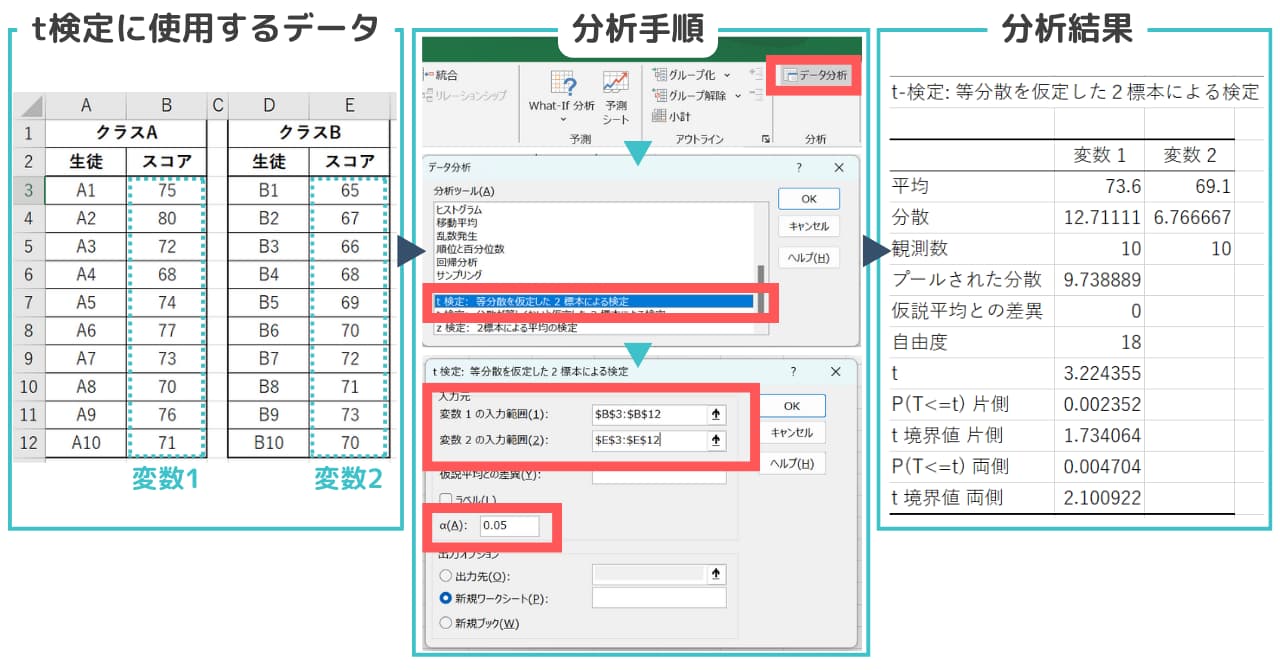
【データ分析ツールを使ったt検定手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「t検定:等分散を仮定した2標本間のt検定」を選択
3.クラスAとクラスBのデータ範囲を選択
4.ラベル(有意水準α)を入力(今回は0.05)
5.「OK」をクリックしてt検定を実行
今回は「差があるかどうか」なので両側検定の値に着目します。結論は、p値(0.0047)が設定した有意水準(0.05)よりも小さいため、帰無仮説(クラスAとクラスBの平均スコアに差がないという仮説)を棄却し、対立仮説(クラスAとクラスBの平均スコアに差がある)を採用します。
≫スチューデントのt検定(等分散を仮定した2標本のt検定)を詳しく解説
エクセルt検定の具体例③|分散が等しくないと仮定した2標本による検定
分散が等しくないと仮定した2標本によるt検定はウェルチのt検定とも呼びます。
2つの異なるグループの従業員に対して異なるトレーニングプログラム(グループ1は新しいトレーニングプログラム、グループ2は従来のプログラム)を実施し、その効果をt検定で判定してみましょう。
帰無仮説:新しいトレーニングプログラムと従来のプログラムの間にパフォーマンススコアの平均に差はない
対立仮説:新しいトレーニングプログラムと従来のプログラムの間にパフォーマンススコアの平均に差がある
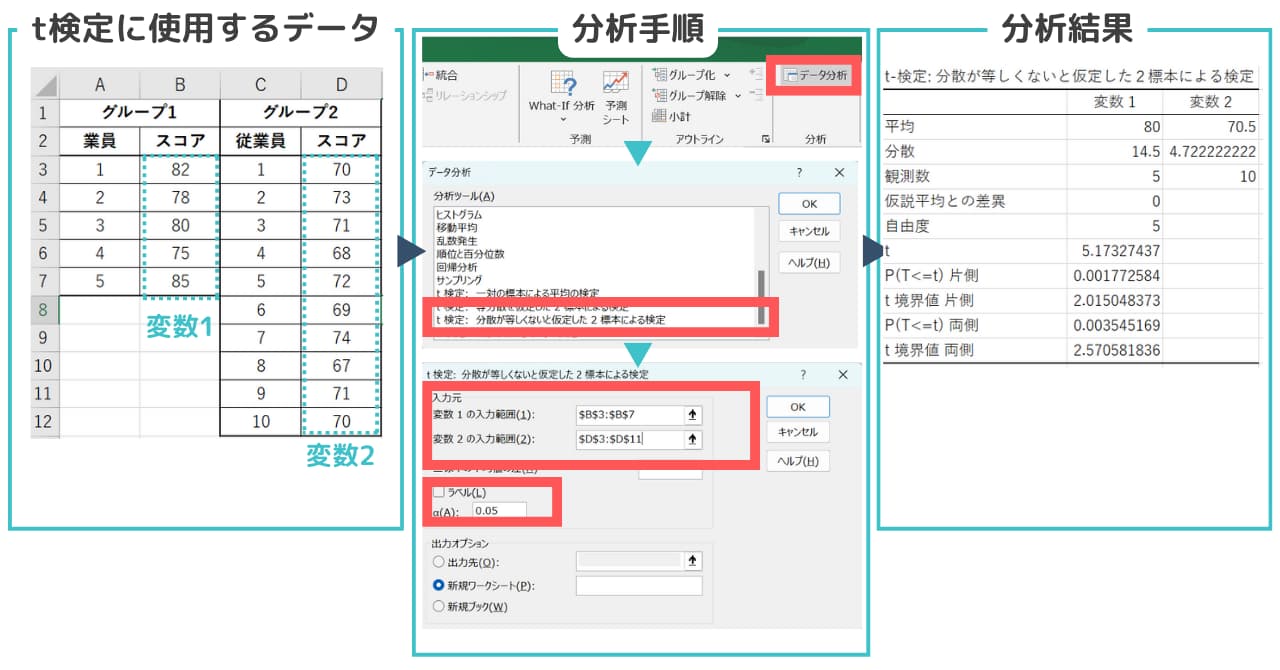
【データ分析ツールを使ったt検定手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「t検定:分散が等しくないと仮定した2標本による検定」を選択
3.グループ1とグループ2のデータ範囲を選択
4.ラベル(有意水準α)を入力(今回は0.05)
5.「OK」をクリックしてt検定を実行
今回は「差があるかどうか」なので両側検定の値に着目します。結論は、p値(0.003545169)が設定した有意水準(0.05)よりも小さいため、帰無仮説(新しいトレーニングプログラムと従来のプログラムの間にパフォーマンススコアの平均に差がない)を棄却し、対立仮説(新しいトレーニングプログラムと従来のプログラムの間にパフォーマンススコアの平均に差がある)を採用します。
≫ウェルチのt検定(等分散が等しくないと仮定した2標本のt検定)を詳しく解説
本書はフルカラーで図や写真がふんだんに使われていて、初学者にとっつきやすく、飽きが来ないように工夫されています。楽しく学べることは一番大事。
読者のつまづきポイントがだいたいわかっていて、本文中で「ん?」となりそうな箇所の後にはすかさず補足情報が入る。
t検定のようなちょっとした統計学を使うビジネスパーソンにはぴったりの一冊です!



