実験計画法とは、「多数の実験条件の組み合わせを総当たりまたは一部の組み合わせで実験を行い、最適な条件を効率よく見つける手法」です。
実験計画法の中でも、一部の水準の組み合わせを行う実験を部分配置実験(直交表など)といい、直交表を使うと実験数を大幅に少なくすることができます。しかし、初めての人には計算方法や水準の割り付け方が複雑で扱いにくいかもしれません。。
そこで、この記事では”3水準の直交表をエクセルを使って実施する手順をできるだけ丁寧にわかりやすく”解説します。
エクセルを使った3水準直交表の作り方 L9の場合
ここでは”3水準直交表を例題で解説(交互作用なしの場合)”の例題を使ってエクセルでの計算手順を解説します。
L9交互作用なしの計算手順【1】事前準備、データの入力
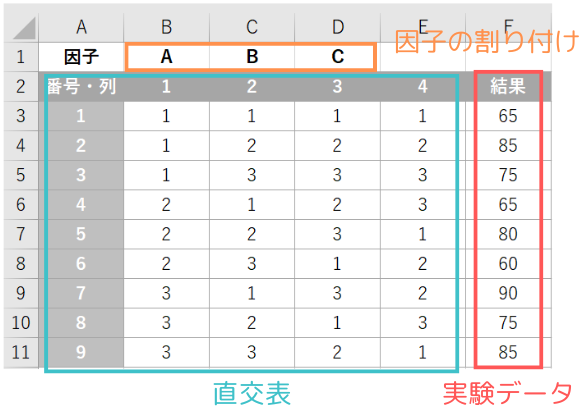
- A2:E11にはL9(34)の直交表を作成
- 因子AはB1(直交表1列目)、因子BはC1(直交表2列目)、因子CはD1(直交表3列目)に割り付け
- F3:F11には実験結果のデータを入力
L9交互作用なしの計算手順【2】各列の各水準ごとの合計を計算

直交表の各列の各水準ごとの合計を計算します。
たとえば、直交表1列目の”水準1”の合計は直交表内の数字”1”と同じ行にある”F3,F4,F5”を合計した値になります。同じように、直交表1列目の”水準2”の合計は直交表内の数字”2”と同じ行にある”F6,F7,F8”を合計した値になります。同様にして、直交表2列目以降も各水準に対応したデータを合計していきます。
B12~B14セルは以下の数式が入ります。入力後C12~E14にコピペすることで各水準の合計が出ます。
”B12セル”=SUMIF(B$3:B$11,1,$F$3:$F$11)
”B13セル”=SUMIF(B$3:B$11,2,$F$3:$F$11)
”B14セル”=SUMIF(B$3:B$11,3,$F$3:$F$11)
L9交互作用なしの計算手順【3】CT,SA,SB,SCの計算
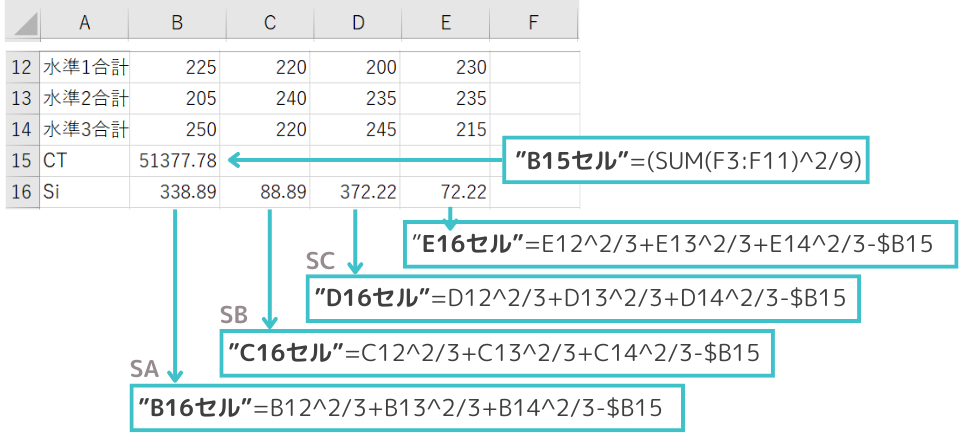
修正項(CT)と各因子の平方和(Si)を計算していきます。
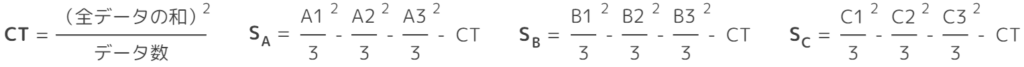
・B15セルは以下の数式が入ります。
”B15セル”=(SUM(F3:F11)^2/9)
・B16~E16セルには以下の式が入ります。
”B16セル”=B12^2/3+B13^2/3+B14^2/3-$B15
”C16セル”=C12^2/3+C13^2/3+C14^2/3-$B15
”D16セル”=D12^2/3+D13^2/3+D14^2/3-$B15
”E16セル”=E12^2/3+E13^2/3+E14^2/3-$B15
L9交互作用なしの計算手順【4】ST,Seの計算
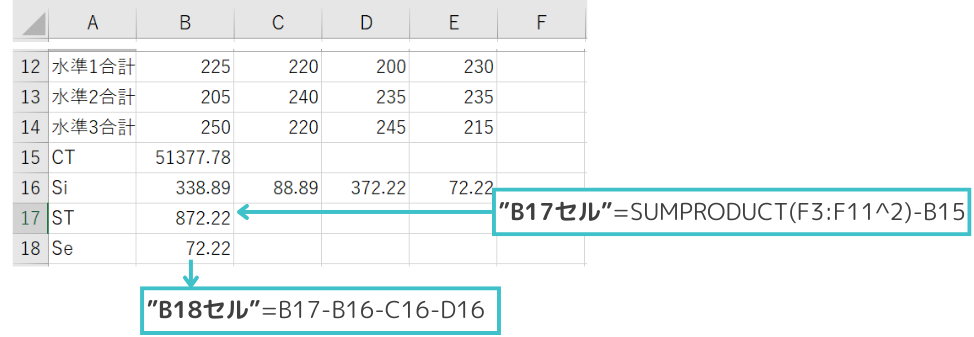
STと誤差項(Se)を計算します。

・B17セルは以下の数式が入ります。
”B17セル”=SUMPRODUCT(F3:F11^2)-B15
・B18セルには以下の式が入ります。
”B18セル”=B17-B16-C16-D16
L9交互作用なしの計算手順【5】分散分析表の作成
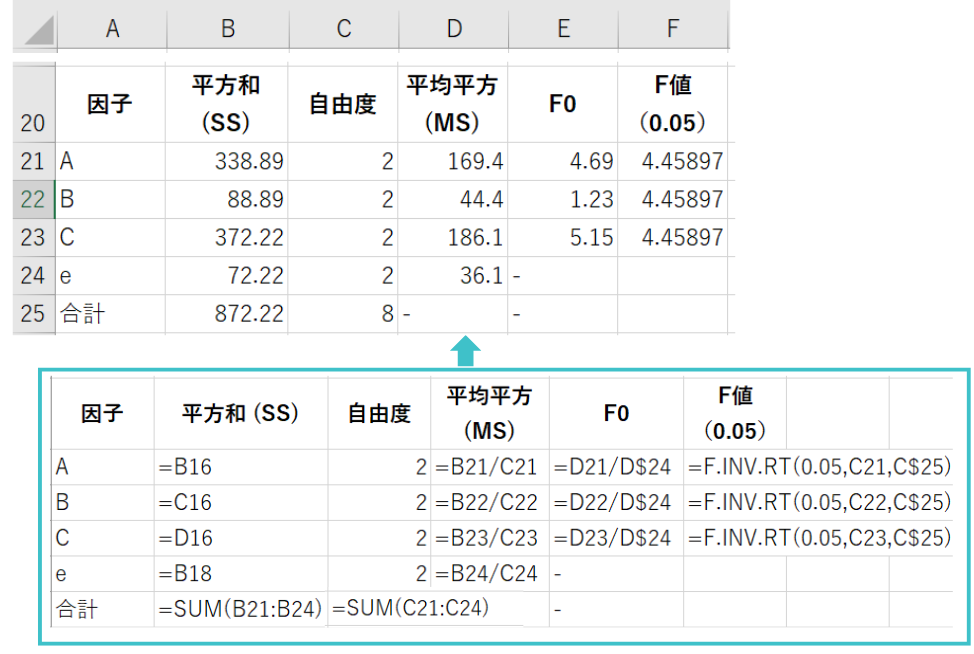
最後にこれまで計算してきた値を使って分散分析表を作成します。各セルの計算式は上記の画像に記載しています。得られたF0とF値を比較して有意差があるかを判定します。
(この例題の結論は”3水準直交表を例題で解説(交互作用なしの場合)”を参照してください。)
L9(34)直交表では交互作用を検証できない理由
例えば因子A、因子B、因子A×Bの交互作用を検証したいとします。L9(34)は4列あるため、1列目に因子A、2列目に因子B、3列目にA×Bの交互作用を割り付ければよいのでは?と考えるかもしれません。しかし、その考えは間違いです。3水準の直交表では1列の自由度は”2”であり、A×Bの交互作用の自由度は”4”になります。したがって、A×Bの交互作用を検証するには”2列”必要になりますが、3列目にA×B交互作用①、4列目にA×B交互作用②を割り付けると4列全てが埋まってしまい、誤差項がなくなってしまいます。これがL9(34)直交表では交互作用が検証できない理由です。