t検定とは？具体例でわかりやすくやり方を解説

t検定とは

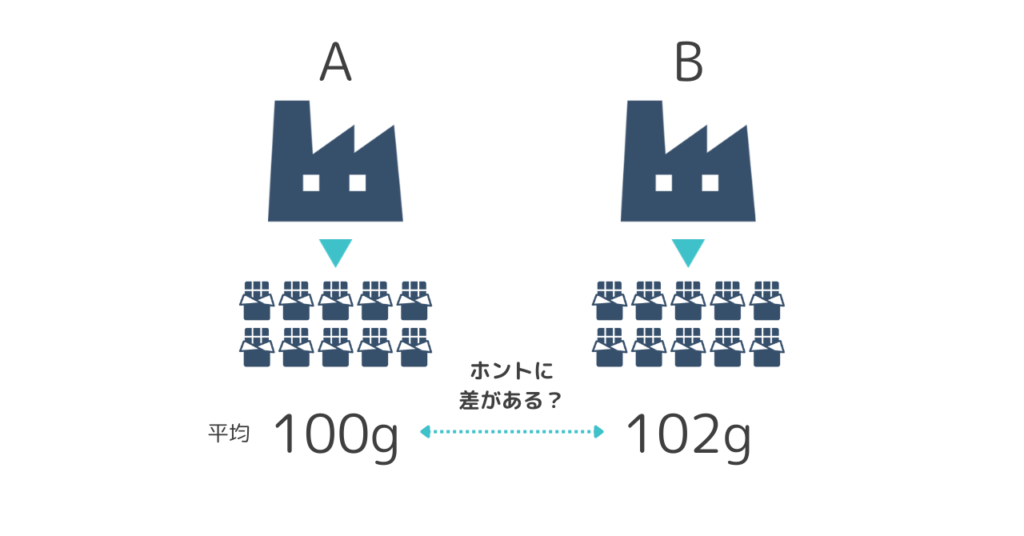
とあるチョコレートを製造している工場が2拠点あります。
2拠点とも同じメーカーの同じ商品です。

それぞれ製品検査のため無作為に製品を10個選び、重量を測定したところ平均値は、工場Aは100g、工場Bは102gでした。

平均値で見ると差があるように見えますが「ぐうぜん平均値に差があっただけ」ではなく、本当にちがいがあるといえるでしょうか？

このように「2つのデータに差があるかどうか」を統計学的に判断するときに使用するのがｔ検定です。

ｔ検定を使うことで、2つのデータそれぞれの母集団の平均値（母平均）が等しいかどうかを統計学的に確かめることができます。

ｔ検定の種類

t検定は大きく分けて3種類に分類され、状況によって使い分ける必要があります。

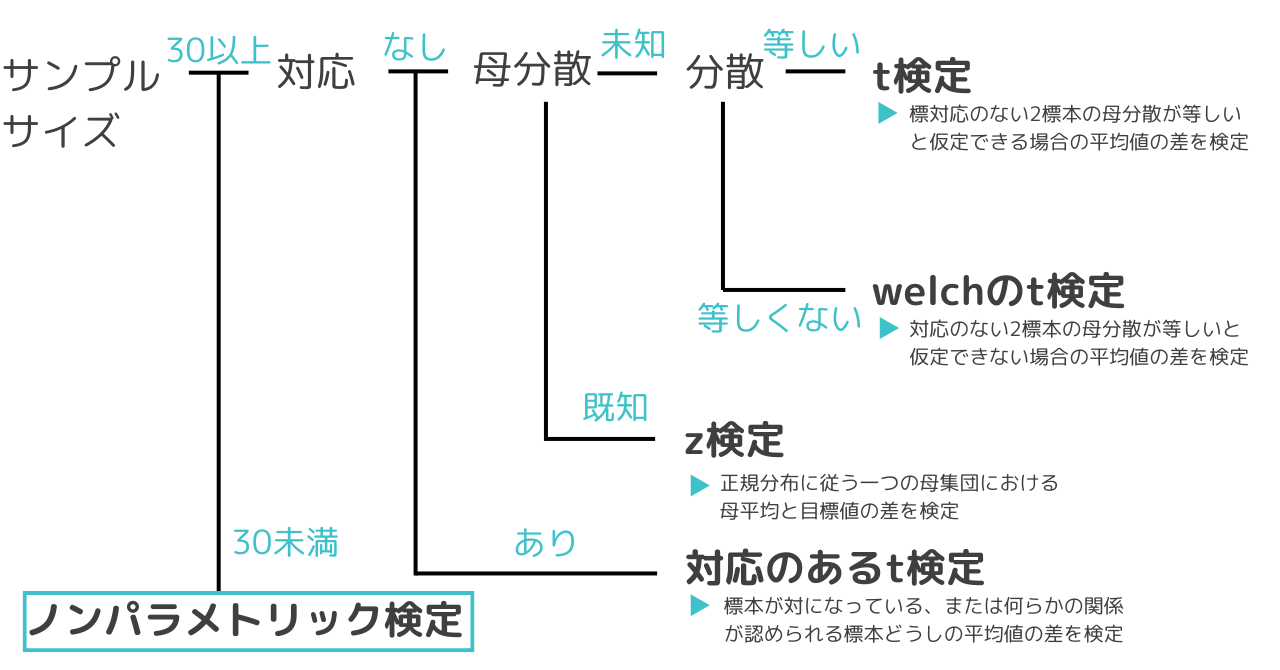
t検定/welchのt検定

２つの独立したグループの平均が異なるかどうかを調べるときに使用します。冒頭に示したチョコレートのお話はこちらの検定に該当します。

対応のあるt検定

関連する２つのグループ（たとえば、同じ被験者の投薬前後の測定値）の平均が異なるかどうかを調べるときに使用します。

z検定

t検定とは違いますがz検定は、2標本の平均値の差（既知の母平均と比較）を比較して差があるかどうかを調べるときに使用します。ただし、母平均が既知の場合は現実的にほとんどないため使用する機会はあまりないでしょう。

ノンパラメトリック検定

t検定、対応のあるt検定、z検定は全て、母集団が正規分布に従うことを前提とした”パラメトリック検定”に分類されます。一方、”ノンパラメトリック検定”とは母集団の分布が正規分布に従うことを仮定しない検定法です。サンプルサイズが小さい場合（30未満）、データの分布が不明の場合に有効な検定方法です。

≫ノンパラメトリック検定

ｔ検定の実施手順

t検定は以下手順で実施します。

帰無仮説と対立仮説を立てる

帰無仮説（H0）は「効果がない」とする仮説で、対立仮説（H1）は「効果がある」とする仮説です。

• 帰無仮説 (H0): 「効果がない」「差がない」といった状態を表します。例えば、２つのグループの平均点が等しいことを示します。
• 対立仮説 (H1): 帰無仮説とは反対の状態を示します。例えば、２つのグループの平均点が異なることを示します。

有意水準を設定する

有意水準は一般的に「α（アルファ）」と表記されます。 帰無仮説をあやまって棄却するリスクの許容度で一般的には0.05（5%）が用いられます。これは、5%の確率で帰無仮説をあやまって棄却するリスク（第一種の過誤）があることを意味します。

検定統計量（ｔ値）の計算方法

データから標本の平均、標準偏差、サンプルサイズを用いてt値を計算します。
t値は以下の公式で計算されます。

$$t=\frac{\bar{x}-\mu}{s/\sqrt{n}}$$

ここで、$\bar{x}$は標本の平均、μ は比較対象の母平均（z検定の場合）または２つの標本平均の差（２標本t検定の場合）、s は標本の標準偏差、n は標本サイズです。

境界値の求め方

有意水準（α）と自由度（サンプルサイズ – 1）を用いて、t分布表から境界値を求めます。

分布の両側に棄却域を設定する検定方式を「両側検定」、片側だけに棄却域を設定する方式を「片側検定」といいます。

例えば、ある規格値の上下限が設定されており、大きすぎても小さすぎてもNGの場合は「両側検定」、下限値だけが設定されており、下限値以下のみNGの場合は「片側検定」といった具合です。

有意水準を5%（0.05）に設定する場合、「両側検定」はα＝0.025のt分布表の値を採用し、「片側検定」はα＝0.05の値を採用します。

自由度	α=0.10	α=0.05	α=0.025	α=0.01	α=0.005
1	6.31	12.71	25.45	63.66	127.32
2	2.92	4.30	6.21	9.92	14.09
3	2.35	3.18	4.18	5.84	7.45
4	2.13	2.78	3.50	4.60	5.60
5	2.02	2.57	3.16	4.03	4.77
6	1.94	2.45	2.97	3.71	4.32
7	1.89	2.36	2.84	3.50	4.03
8	1.86	2.31	2.75	3.36	3.83
9	1.83	2.26	2.69	3.25	3.69
10	1.81	2.23	2.63	3.17	3.58

判定

ｔ分布表から臨界値を求め、棄却域を設定する。そして検定統計量が、
・棄却域に入る　→　帰無仮説を棄却
・棄却域に入らない　→　帰無仮説を採択

t検定のやり方を具体例でわかりやすく解説

「2標本のt検定（対応あり、なし）」の具体例を見ていきましょう。

2標本のt検定　対応ありの具体例

≫対応のあるt検定を詳しく解説

2標本のt検定　対応なしの具体例

≫スチューデントのt検定（等分散を仮定した対応のない2標本のt検定）を詳しく解説
≫ウェルチのt検定（等分散を仮定しない対応のない2標本のt検定）を詳しく解説

z検定の具体例