今回は、エクセルを使って対応のある2標本のt検定を「データ分析」を使用せずに関数と計算のみで実行する方法を解説します。
【この記事でわかること】
・対応のある2標本のT検定を関数を使って計算する方法
では早速具体例を用いてエクセルでt検定を実行してみましょう。
エクセルで関数を使った「対応のある2標本のt検定」計算例
ある企業で従業員の生産性を向上させるための新しいトレーニングプログラムを導入したとします。トレーニング前後の生産性スコアを比較して、プログラムの効果をt検定で判定してみましょう。
使用するデータ
計算に使用するデータは以下の表になります。1列目には従業員ナンバー、2列目にはトレーニング前の生産性スコア、3列目にはトレーニング後の生産性スコアを示しています。この表をエクセルの”A1セル”に貼り付けてください。
| 従業員 | トレーニング前 | トレーニング後 |
|---|---|---|
| 1 | 70 | 75 |
| 2 | 65 | 68 |
| 3 | 80 | 85 |
| 4 | 75 | 78 |
| 5 | 60 | 65 |
| 6 | 70 | 73 |
| 7 | 68 | 72 |
| 8 | 74 | 77 |
| 9 | 72 | 76 |
| 10 | 69 | 74 |
ちなみに今回検証するデータの帰無仮説、対立仮説は以下になります。
帰無仮説:トレーニングプログラムで生産性は向上しない
対立仮説:トレーニングプログラムは生産性が向上する
STEP1.差分を求める
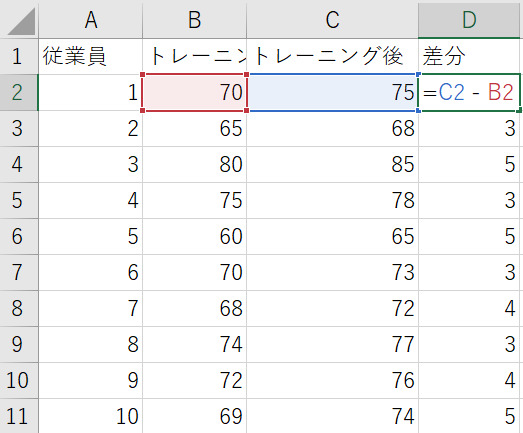
トレーニング前後の数値の差分を求めます。
トレーニング後の値からトレーニング前の値を引いて求めるため、”D2セル”に”=C2-B2”を入力します。D3~D11セルまで同様にして差分を求めます。
STEP2.差分の平均値を求める
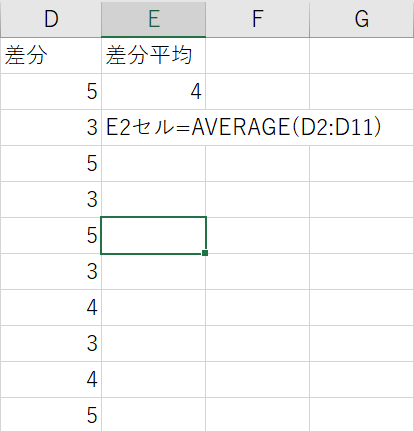
STEP1で求めたトレーニング前後の差分の平均値を求めます。
平均値の計算は関数の”AVERAGE”を使います。”E2セル”に”=AVERAGE(D2:D11)”と入力し、差分の平均値を算出します。
STEP3.差分の標準偏差を求める

STEP2で求めた差分の平均値から標準偏差を求めます。
標準偏差の計算は関数の”STDEV.S”を使います。”F2セル”に”=STDEV.S(D2:D11)”と入力し、差分の標準偏差を算出します。
STEP4.t値を求める

差分の標準偏差と平均値、データ数からt値を求めます。
”G2セル”に”=E2 / (F2 / SQRT(COUNT(D2:D11)))”と入力し、t値を算出します。
STEP5.自由度を求める

データの個数から自由度を求めます。
自由度はデータの個数-1なので”H2セル”に”=COUNT(D2:D11) – 1”と入力し、自由度を算出します。
STEP6.p値を求める

t値と自由度からエクセルの関数”T.DIST.2T”を使ってp値を求めます。
”I2セル”に”=T.DIST.2T(ABS(G2), H2)”と入力し、p値を算出します。
以上でt検定の計算が完了です。今回の結果ではp値が有意水準(α)を0.05とすると、p値はこの有意水準よりもはるかに小さいため、帰無仮説を棄却します。つまり、トレーニング前後のスコアに統計的に有意な差があると結論付けることができます。
データ分析を使用して確認
エクセルにはアドイン機能でt検定などの分析を自動で実行してくれる「分析ツール」があります。今回のデータを分析ツールを使って分析して確認してみましょう。
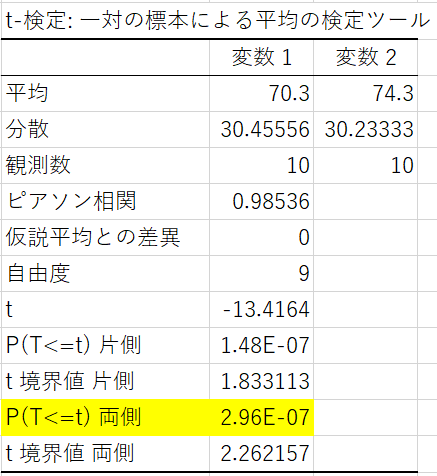
手動で計算した結果と同じ値になっているため、正確に計算できていることが確認できました。



