回帰分析は、従属変数(目的変数:予測したいデータ)に独立変数(説明変数:予測に必要なデータ)がどれだけの影響を与えるのかを予測する方法です。エクセルではアドイン機能の分析ツールを使えば簡単に回帰分析をすることができます。
回帰分析の目的は、データから関係性をモデル化し、そのモデルを使って将来の値を予測することです。回帰分析を使いこなせば、売上、顧客行動の分析、科学実験の結果などを予測することができます。
回帰分析には種類があり、この記事では独立変数が1つからなる単回帰分析と2つ以上からなる重回帰分析をExcelの分析ツールを使った分析手順、結果の見方を解説します。
【この記事でわかること】
・エクセル「分析ツール」を使って単回帰分析、重回帰分析をする方法
・回帰分析結果の見方と意味
エクセル「分析ツール」を使った単回帰分析のやり方と具体例
今回の回帰分析は”従業員の経験年数”と”年収”に関するデータを使用して説明します。データはchatGPTを使って生成した仮想データです。
データの内容
・従属変数(目的変数):予測したい変数。ここでは「年収」。
・独立変数(説明変数):従属変数に影響を与えると考えられる変数。ここでは「経験年数」。
分析ツールの有効化
エクセルで回帰分析を行うためには、「分析ツール」を有効にする必要があります。このツールはデフォルトでは有効化されていないことが多いので、まずは「データ分析」ツールを有効化する必要があります。
データ分析ツールの有効化手順
- Excelを開き、上部にある「ファイル」タブをクリックします。
- メニューの一番下にある「オプション」を選択します。
- 左側のメニューから「アドイン」カテゴリを選択し、「分析ツール」を見つけます。
- 下部の「管理」ボックスで「Excelアドイン」を選択し、「設定」をクリックします。
- 表示されるリストから「分析ツール」にチェックを入れ、「OK」をクリックします。
これで、分析ツールが使用可能になります。
エクセルの分析ツールを使った単回帰分析手順
次に、具体的な回帰分析の手順を説明します。
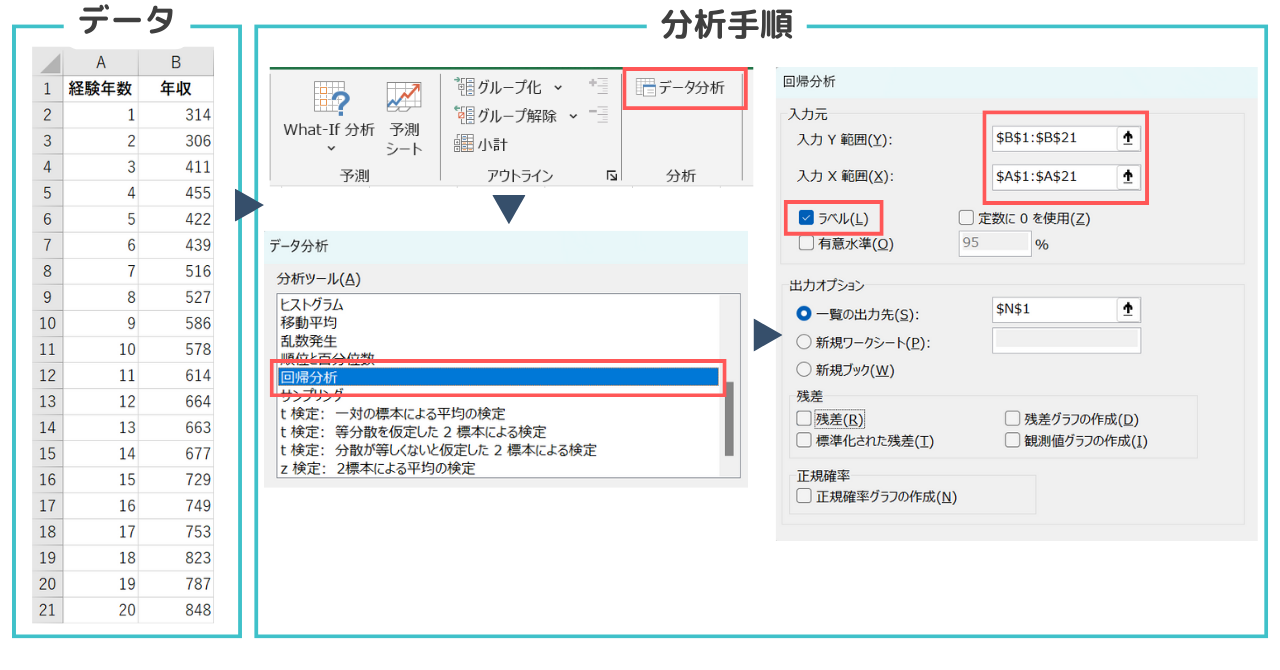
単回帰分析の手順
- データ分析ツールを選択:Excelの「データ」タブに移動し、右端にある「データ分析」を選択
- 回帰分析を選択:表示されるリストから「回帰分析」を選択
- 入力範囲の指定:
- 入力Y範囲:従属変数(年収)を含むセル範囲を選択(例:$B$1:$B$21)
- 入力X範囲:独立変数(経験年数)を含むセル範囲を選択(例:$A$1:$A$21)
- ラベル:データの最初の行にラベルが含まれている場合は、「ラベル」にチェック(例では経験年数(A1)、年収(B1)がラベルです)
- 出力オプションの指定:
- 出力範囲:分析結果を表示するセル範囲を指定(例:$D$1)
- その他のオプションは必要に応じて選択します。
- OKをクリック:設定が完了したら、「OK」ボタンをクリック。エクセルが回帰分析を実行し、指定したセル範囲に結果を出力します。
回帰分析結果の見方
エクセルで回帰分析を実行すると、結果が指定したセル範囲に統計情報が出力されます。
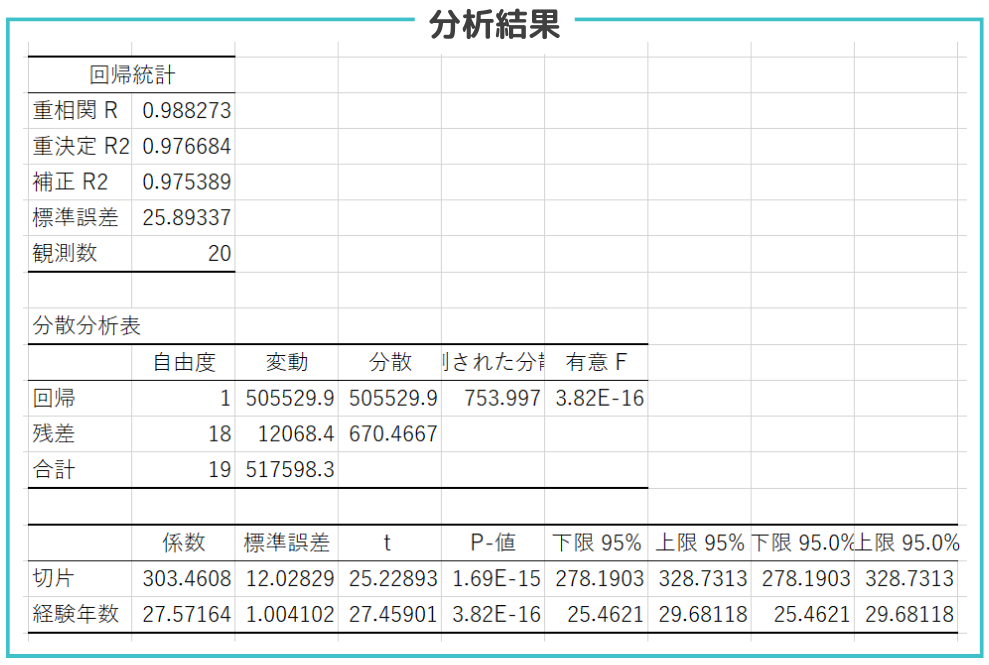
分析結果の見方
- 回帰統計:
- 重相関R: 相関係数であり、従属変数と独立変数の間の相関の強さを示します。1に近いほど強い相関があります。
- 重決定R²: 決定係数であり、モデルが従属変数の変動をどれだけ説明できるかを示します。0から1の間の値を取り、1に近いほどモデルの説明力が高いことを示します。
- 補正R²: R²を調整したもので多くの変数を含むモデルで過大評価を避けるために使用されます。標本の数が増加すると決定係数が上昇するため自由度で調整しています。重回帰分析でよく用いられます。
- 分散分析(ANOVA):
- 回帰: 回帰モデルによって説明される変動を示します。
- 残差: 回帰モデルでは説明できない変動を示します。
- 合計: 総変動量を示します。
- 観測された分散比(F値): 回帰モデル全体の有意性を示す指標です。F値が高いほど、モデルが有意である可能性が高いです。
- 有意 F(有意確率): F値に対するp値で、「説明変数の組み合わせに意味はない」という確率を表すものです。通常は0.05未満であればモデルが有意であると判断します。
- 回帰係数:
- 係数: 傾きと切片を表しています。y=ax+bのaが傾き、bが切片です。
- 標準誤差: 係数の標準誤差を示し、係数の精度を測る指標です。
- t値: 係数の有意性を示す統計量です。t値が大きいほど係数が有意である可能性が高いです。
- P値: 係数の有意性を示すp値で、通常は0.05未満であれば係数が有意であると判断します。説明変数のp値はANOVAの有意Fと同じ値です。
回帰分析結果の見方補足
- 回帰方程式の解釈
今回の回帰分析の結果から得られる回帰方程式は以下のようになります。
y = 27.57164x + 303.4608
この式を使って、従業員の経験年数(x)に基づいて年収を予測することができます。 - 決定係数 (R²) の意味
R²は、独立変数が従属変数の変動をどれだけ説明できるかを示す指標です。例えば、R²が0.8であれば、独立変数が従属変数の変動の80%を説明していることになります。 - p値と有意性の判断
通常、p値が0.05未満であれば、その結果は有意であると判断されます。これは、95%の信頼度でその結果が偶然ではないことを示しています。今回の例では”3.82E-16″と非常に小さい値なので帰無仮説(説明変数(経験年数)が目的変数(年収)に影響を与えない)を棄却できます。
エクセルの分析ツールを使った”重回帰分析”手順
次に変数が2つ以上ある場合の重回帰分析の手順をご紹介します。やり方はほとんど単回帰分析を同じで、例では変数が2つに増えているため指定する”X範囲”が変わります。
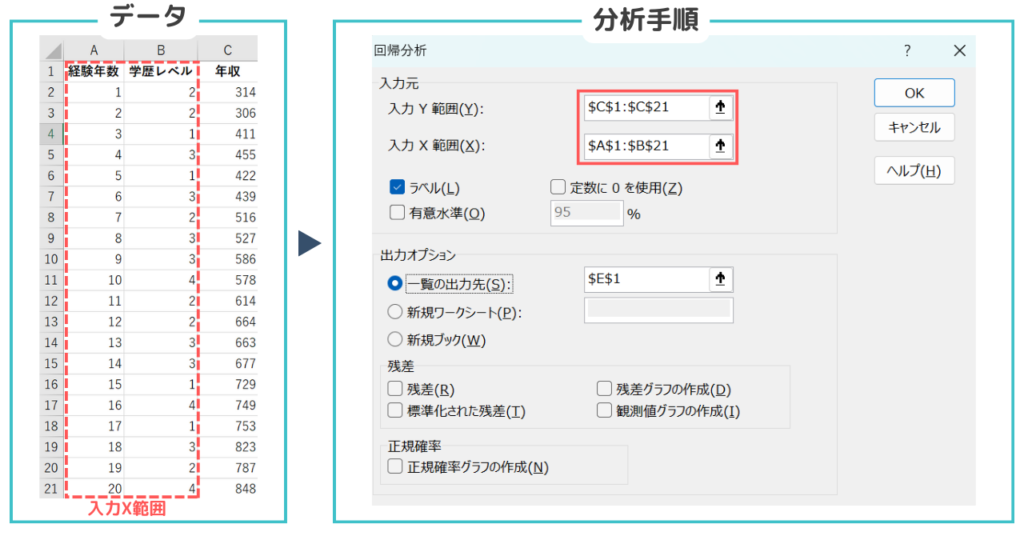
重回帰分析の手順
- データ分析ツールを選択:Excelの「データ」タブに移動し、右端にある「データ分析」を選択
- 回帰分析を選択:表示されるリストから「回帰分析」を選択
- 入力範囲の指定:
- 入力Y範囲:従属変数(年収)を含むセル範囲を選択(例:$C$1:$C$21)
- 入力X範囲:独立変数(経験年数、学歴レベル)を含むセル範囲を選択(例:$A$1:$B$21)
- ラベル:データの最初の行にラベルが含まれている場合は、「ラベル」にチェック
- 出力オプションの指定:
- 出力範囲:分析結果を表示するセル範囲を指定(例:$D$1)
- その他のオプションは必要に応じて選択します。
- OKをクリック:設定が完了したら、「OK」ボタンをクリック。エクセルが回帰分析を実行し、指定したセル範囲に結果を出力します。
”重回帰分析”結果の見方
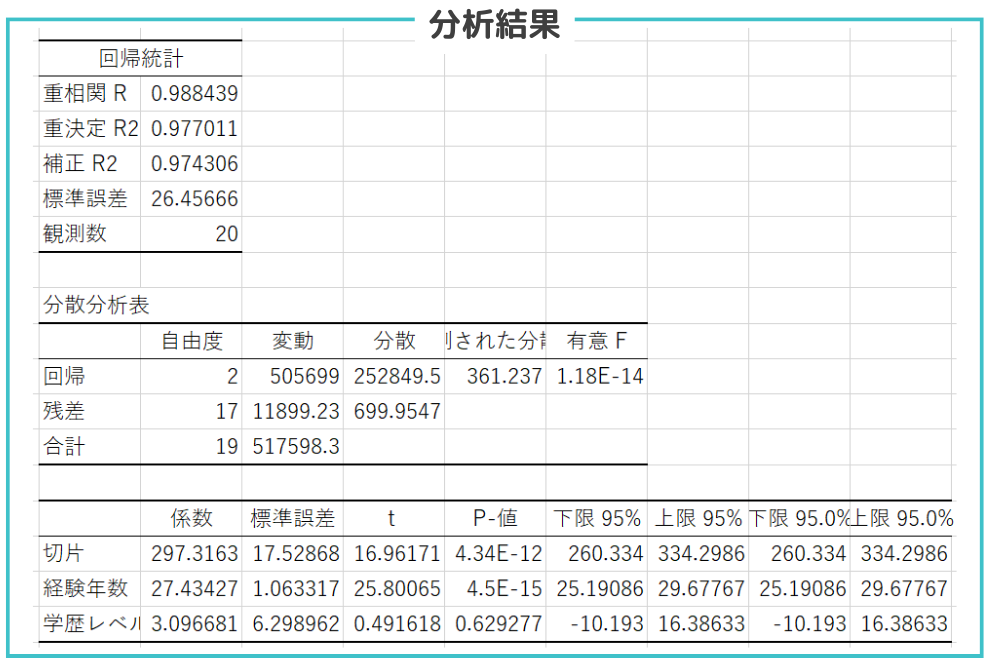
重回帰分析結果の見方も基本的には単回帰分析と同じです。異なる点は一番下の行に変数が1つ追加されている点です。今回の例では学歴レベルのp値が”0.62977”と大きいため帰無仮説を棄却できない、つまり「学歴レベルが年収に影響を与えていない可能性が高い」と考えられます。
例の回帰式は以下になります。
y = 27.43427×1 + 3.096681×2 + 297.3163
この式を使って、従業員の経験年数(x1)、学歴レベル(x2)に基づいて年収を予測することができます。
また、標本の数が増加すると決定係数が上昇するため自由度で調整した補正R2も確認するようにしましょう。


