この記事ではExcelで「データ分析ツール」を使用した分散分散のやり方を具体例を使って紹介します。
【この記事でわかること】
・エクセルを使った一元配置分散分析のやり方
・エクセルを使った繰り返しのある二元配置分散分析のやり方
・エクセルを使った繰り返しのない二元配置分散分析のやり方
・どの分散分析を使ったらよいか
エクセル一元配置分散分析の準備
Excelには「データ分析」ツールがあり、これを使うと簡単にt検定を実施できます。ただし、このツールはデフォルトでは有効化されていないことが多いので、まずは「データ分析」ツールを有効化する必要があります。
【データ分析ツールの有効化手順】
1. Excelを開き、「ファイル」タブをクリックします。
2.「オプション」を選択します。
3.「アドイン」カテゴリを選択し、「分析ツール」を見つけます。
4.「Excelアドイン」を選択し、「設定」をクリックします。
5.「分析ツール」にチェックを入れ、「OK」をクリックします。
分散分析で使う用語
分散分析では頻繁に以下の用語が出てきますのでついでに覚えておきましょう。
- 要因(Factor)
実験や調査で結果に影響を与えると考えられるもののことです。例えば、植物の成長速度に影響を与える要因として、「水やりの頻度」や「日光の量」が考えられます。実験では、これらの要因がどのように植物の成長に影響するかを調べることになります。 - 因子(Factor)
「要因」の中から実験や調査の結果に影響を及ぼす変数のことを指します(つまり要因の中から選んだ一つ)。例として、「肥料の種類」が植物の成長に与える影響を調べる場合、「肥料の種類」は一つの因子になります。 - 水準(Level)
因子が取りうる値や状態のことを指します。因子が「水やりの頻度」であれば、その水準は「1日に1回」、「1日に2回」、「1日に3回」といった具体的な値になります。つまり、実験で変化させる因子の具体的な設定のことです。
エクセル分散分析の種類
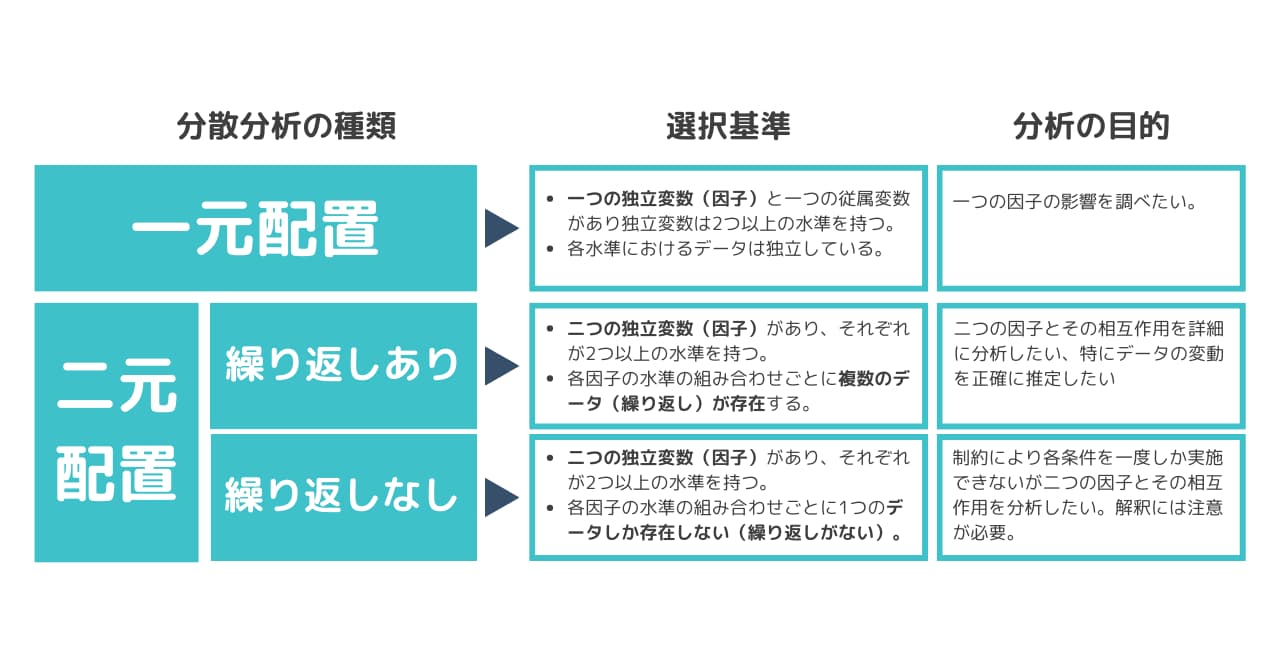
エクセルの分散分析は大きく分けると以下の3種類があり、エクセルの分析ツールでも各分散分析に対応した分析方法を選択する必要があります。
- 分散分析:一元配置
▶分析目的:1つの因子の影響を調べたい - 分散分析:繰り返しのある二元配置
▶分析目的:2つの因子とその交互作用を詳細に分析したい。 - 分散分析:繰り返しのない二元配置
▶分析目的:制約により各操作を一度しか実施できないが、2つの因子とその交互作用を分析したい。
具体例でエクセル分散分析のやり方を解説
エクセルでの分散分析は以下の手順で進めていきます。
【データ分析ツールの分散分析手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「分散分析」を選択
(例:「分散分析:一元配置」)
3.比較するデータ範囲、出力範囲、その他オプションを指定
4.「OK」をクリックして分散分析を実行
では、実際にエクセルを使った分散分析のやり方を種類ごとに見ていきましょう。
エクセルで分散分析:一元配置
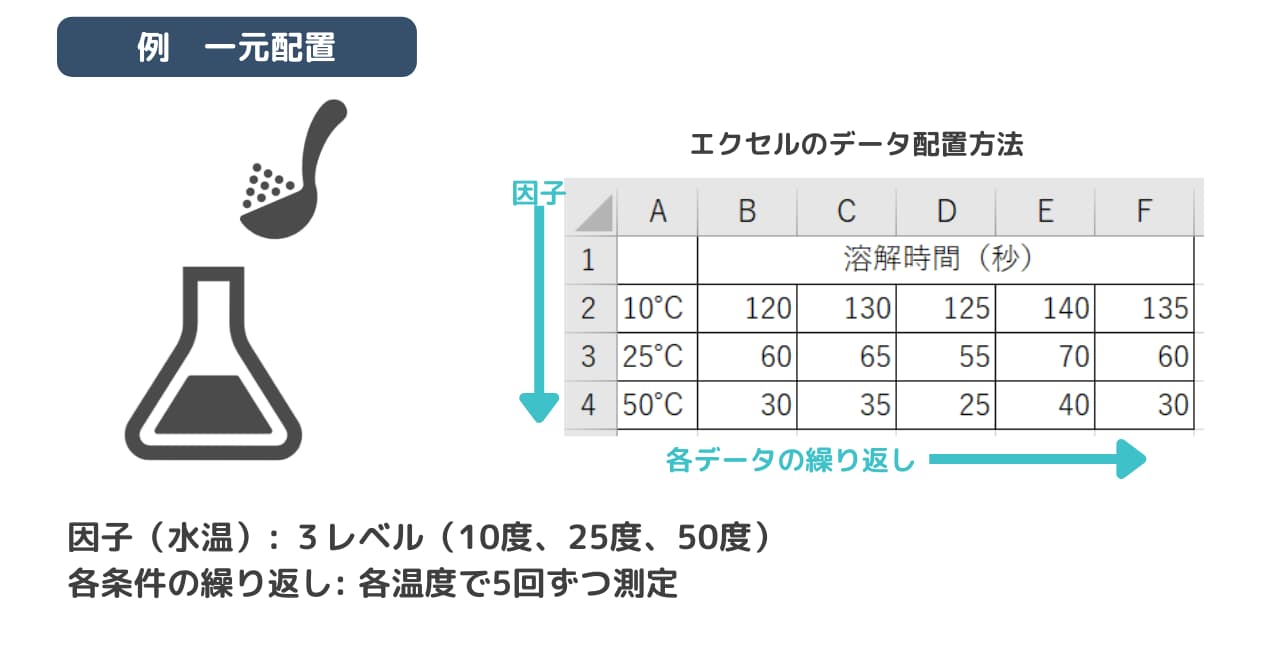
3種類の異なる温度(冷温、常温、温湯)が溶解速度にどのような影響を与えるかを調べます。
今回は砂糖が水にどれだけ早く溶けるかを計測し、温度が溶解時間に影響するか検証します。
検討の因子、繰り返し回数は以下とします。
因子(水温): 3レベル(10度、25度、50度)
各条件の繰り返し: 各温度で5回ずつ測定
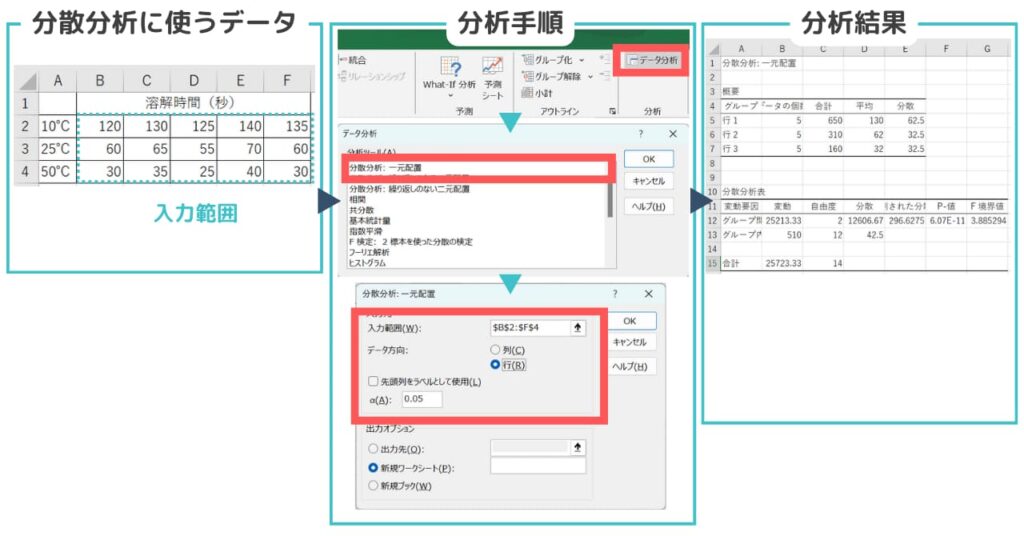
【エクセルを使った一元配置分散分析の実行手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「分散分析:一元配置」を選択
3.データの入力範囲を選択(例はB2~F4を選択)
4.データの入力方向を選択(例は各データを横方向に入力しているので「行」を選択)
5.有意水準αを入力(今回は0.05)
6.「OK」をクリックして分散分析を実行
【分散分析結果の解釈】
今回、分散分析で得られたP-値はα(0.05)よりも非常に小さいため、因子(水温)の影響が統計的に有意であり、溶解時間が変わることを意味しています。
≫一元配置分散分析をPythonで実行
≫一元配置分散分析を例題でわかりやすく解説
エクセルで分散分析:繰り返しのある二元配置
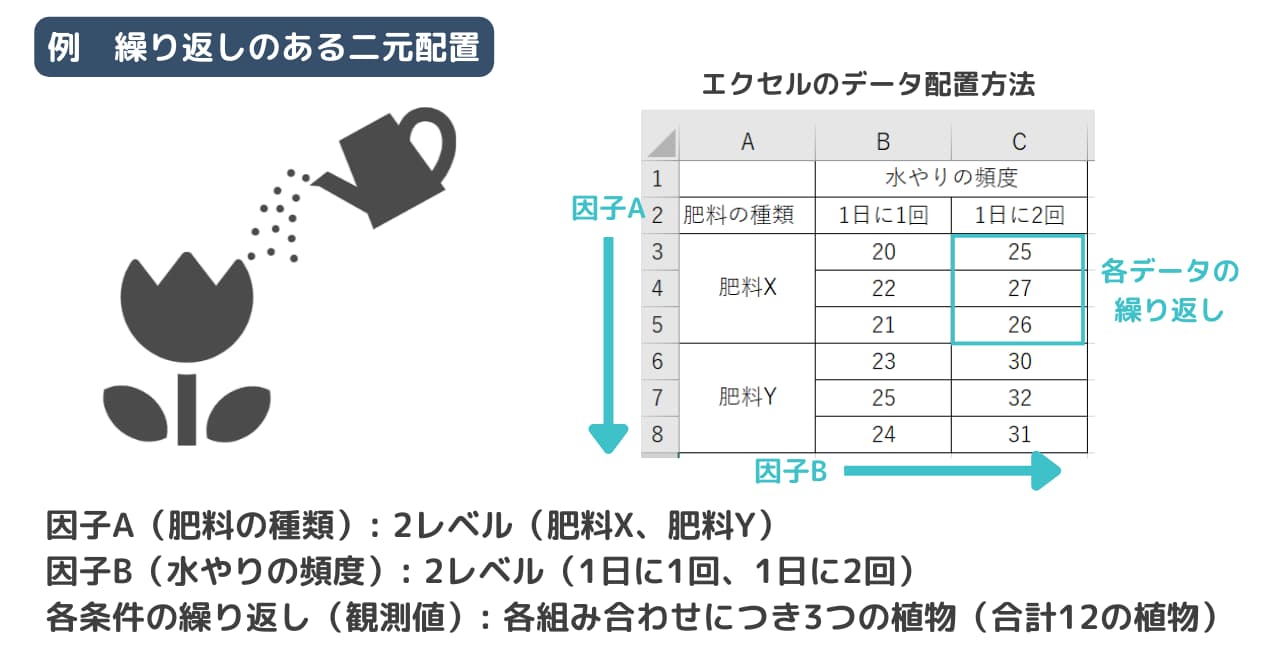
植物の成長に影響を与える2つの因子「肥料の種類」と「水やりの頻度」を検討します。
目的はこれらの因子とその相互作用が植物の成長高にどのように影響するかを調べることです。
検討の因子、繰り返し回数は以下とします。
因子A(肥料の種類): 2レベル(肥料X、肥料Y)
因子B(水やりの頻度): 2レベル(1日に1回、1日に2回)
各条件の繰り返し(観測値): 各組み合わせにつき3つの植物(合計12の植物)
エクセルにデータを入力するときは、因子Aは列、因子Bを行にとり、同一水準での繰り返しは行に配置してください(上の画像を参照)。このように配置しなければエクセルのデータ分析を正確に使うことができないので注意が必要です。
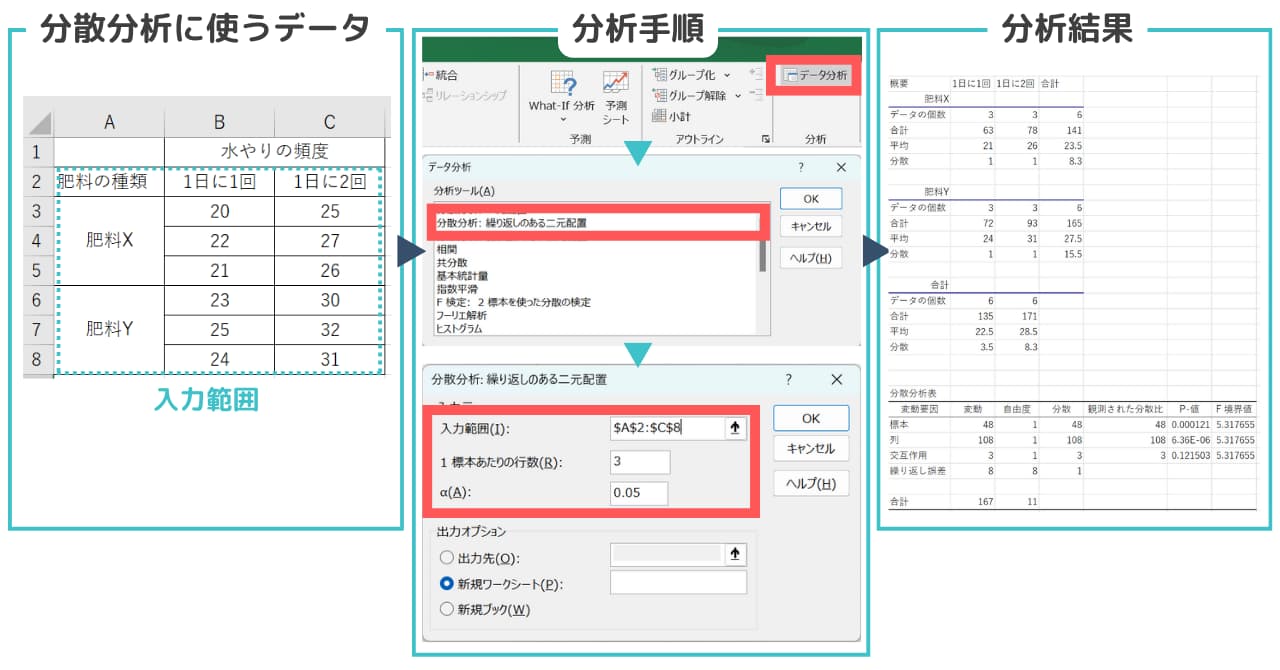
【エクセルを使った繰り返しのある二元配置の実行手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「分散分析:繰り返しのある二元配置」を選択
3.データの入力範囲を選択(例はA2~C8を選択)
4.1標本当たりの行数を入力(例は繰り返し3回なので「3」)
5.有意水準αを入力(今回は0.05)
6.「OK」をクリックして分散分析を実行
【分散分析結果の解釈】
・変動要因:標本
この行は標本(因子A)の変動を表していて、この因子がデータに与える影響の大きさを示しています。P-値が0.05よりも小さいため、因子Aの影響は統計的に有意であると結論付けられます。
・変動要因:列
この行は列(因子B)の変動を表していて、因子Bがデータに与える影響の大きさを示しています。非常に小さいP-値は、因子Bの影響も統計的に有意であることを意味します。
・交互作用
この行は2つの因子AとBの交互作用の変動を示しています。P-値が0.05よりも大きいため、因子AとBの交互作用は統計的に有意ではないと結論付けられます。つまり、両因子の組み合わせによる影響は統計的には確認できませんでした。
・結論
分散分析の結果から、因子A(肥料の種類)と因子B(水やりの頻度)はそれぞれ統計的に有意な影響を与えているが、交互作用は有意ではないことがわかりました。
≫繰り返しのある二元配置分散分析をPythonで実行
≫繰り返しのある二元配置分散分析を例題でわかりやすく解説
エクセルで分散分析:繰り返しのない二元配置
注意点として、試行回数が少ないため結果の信頼性が劣ります。そのため基本的には試行回数を増やし、繰り返しのある二元配置での分析をおすすめします。
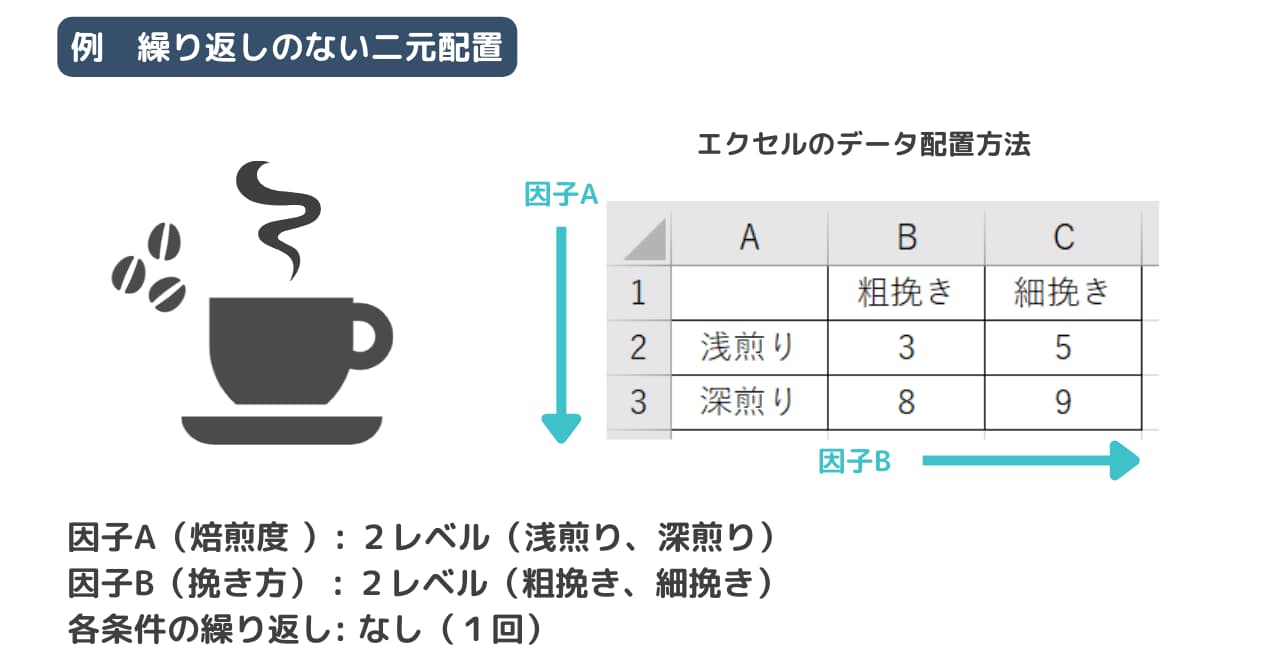
コーヒーの風味が豆の焙煎度と挽き方によってどのように変わるかを調べてみましょう。焙煎度は「浅煎り」と「深煎り」の2種類、挽き方は「粗挽き」と「細挽き」の2種類で検証するとします。これらの条件でコーヒーを抽出し、10点満点で風味を評価した結果を分散分析で解析してみましょう。
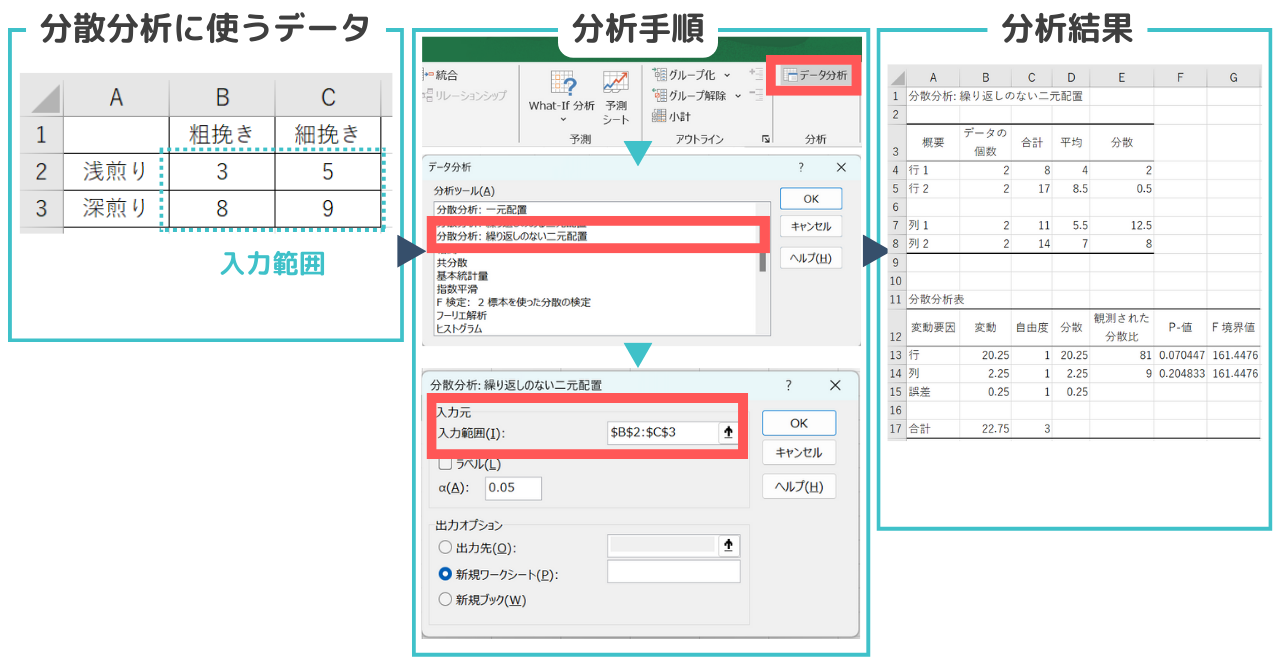
【エクセルを使った繰り返しのない二元配置の実行手順】
1. Excelの「データ」タブに移動し、「データ分析」をクリック
2.表示されるリストから「分散分析:繰り返しのない二元配置」を選択
3.データの入力範囲を選択(例はB2~C3を選択)
4.有意水準αを入力(今回は0.05)
5.「OK」をクリックして分散分析を実行
【分散分析結果の解釈】
・変動要因:標本
この行は標本(因子A:焙煎度)の変動を表していて、通常の有意水準0.05をわずかに超えています。これは、焙煎度がコーヒーの風味評価に与える影響が統計的に有意でない可能性を示唆していますが、非常にギリギリの結果です。
・変動要因:列
この行は列(因子B:挽き方)の変動を表していて、有意水準0.05よりもかなり高いです。この結果は、挽き方が風味評価に統計的に有意な影響を与えていないことを示しています。
・結論
コーヒーの風味評価において焙煎度と挽き方は統計的に有意な影響を与えていないことが示されています。ただし、焙煎度に関してはp値が0.05に近いため、より多くのデータを集めて再分析を行うと異なる結果になる可能性があります。挽き方はp値がかなり高いため、この因子は風味にあまり影響を与えていないと考えられます。



