t検定では2標本の平均値に差があるかどうかを判定する場合に使用します。分散分析は3水準以上からなるデータや2因子のデータの平均を統計的に判断できる有力なツールです。
Excelを使って分散分析をやることもできますが、Pythonを使っても簡単に分散分析を実行することができ、2因子以上の分析も可能です。この記事では、一元配置、二元配置の分散分析をPythonを使って分析する方法をわかりやすく解説します。
Pythonを使って「一元配置分散分析」
例として、3種類の異なる温度(冷温、常温、温湯)が溶解速度にどのような影響を与えるかを調べます。今回は砂糖が水にどれだけ早く溶けるかを計測し、温度が溶解時間に影響するか検証します。
今回の検証は因子が一つ(水温)なので一元配置分散分析を行いましょう。
以下が一元配置分散分析を実行するコードです。
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# CSVファイルのデータを読み込む
data = pd.read_csv("one-way-data.csv")
# olsモデルで分散分析を実行するための式を定義(式を修正)
formula = 'result ~ facter'
model = ols(formula, data=data).fit()
# 分散分析の結果を計算
aov_table = anova_lm(model, typ=2)
aov_table.columns = ["平方和", "自由度", "F値", "p値"]
# 結果を表示
print(aov_table)インポートファイルの注意点
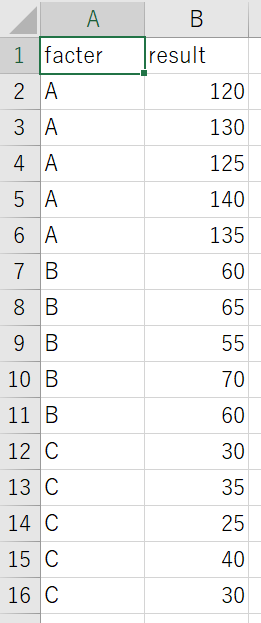
今回は「one-way-data.csv」というファイルを読み込み分析するプログラムになっています。
インポートするデータの注意点としては、画像のようにA列には因子、B列には結果を入力してください。
例題では因子が水温(A=冷温、B=常温、C=温湯)であり、結果は砂糖の溶解速度です。
コードの実行結果
実際にコードを実行してみましょう。
実行すると左から平方和、自由度、F値、p値が表示されます(日本語に変換しているため列がややずれています)。

例題の結論としては、分散分析で得られたp値はα(0.05)よりも非常に小さいため、因子(水温)の影響が統計的に有意であり、溶解時間が変わること結論付けることができます。
Pythonを使って「繰り返しのある二元配置分散分析」
例として、植物の成長に影響を与える2つの因子「肥料の種類」と「水やりの頻度」を検討します。
目的はこれらの因子とその相互作用が植物の成長高にどのように影響するかを調べることです。
今回の検証は因子が2つ(肥料の種類、水やりの頻度)なので二元配置分散分析を行いましょう。
以下が二元配置分散分析を実行するコードです。
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.graphics.factorplots import interaction_plot
# CSVファイルのデータを読み込む
data = pd.read_csv("two-way-data.csv")
#グラフ化
fig = interaction_plot(data.facter_1, data.facter_2, data.result,
colors=['red','blue'], markers=['o','^'], ms=10)
# olsモデルで分散分析を実行するための式を定義
formula = 'result ~ C(facter_1) + C(facter_2) + C(facter_1):C(facter_2)'
model = ols(formula, data=data).fit()
# 分散分析の結果を計算
aov_table = anova_lm(model, typ=2)
aov_table.columns = ["平方和", "自由度", "F値", "p値"]
# 結果を表示
print(aov_table)インポートファイルの注意点

今回は「two-way-data.csv」というファイルを読み込み分析するプログラムになっています。
インポートするデータの注意点としては、画像のようにA列には因子A、B列には因子B、C列には結果を入力してください。
例題では因子Aが肥料の種類(A、B)、因子Bが水やりの頻度(1回、2回)であり、結果は植物の成長高です。
コードの実行結果
実際にコードを実行してみましょう。
実行すると左から平方和、自由度、F値、p値が表示されます(今回は日本語に変更していないパターン。列がずれないのでこちらのほうが見やすいかもしれません。)。
加えて、因子の差を視覚的にわかりやすいように各水準の平均値をグラフで表示するコードになっています。
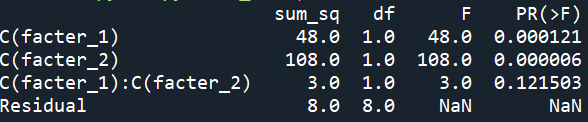
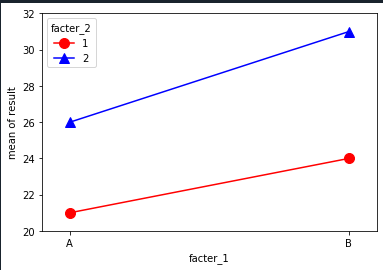
例題の結論としては、分散分析の結果から、因子A(肥料の種類)と因子B(水やりの頻度)はそれぞれ統計的に有意な影響を与えているが、交互作用は有意ではないと結論付けることができます。

