科学的な研究や実験を行う方は、効率よく、客観的な分析を行いたいと考えると思います。この記事ではそれをかなえる”実験計画法”について、数式や細かい技術的な詳細に入る前に基本的な概念について解説します。
”実験計画法”とは
実験計画法とは、①どのような実験を行えば効率的に目的とするデータが得られるか、②得られた実験データをどのように解析すれば客観的な結論を出せるか、この2つのことを取り扱う学問です。
実験計画法の目的は、時間や場所、予算などの制約の中で実験の検出力を最大し、データに基づいて客観的な結論を出すことです。
この記事では、以下3つの項目に分けて実験計画法の概要について解説していきます。
- 実験の組み方
- 実験の場の管理の考え方
- 実験データの解析の仕方
”品質管理と実験計画法の基礎が学べる”
『品質管理のための実験計画法テキスト』は、統計の基礎から分散分析、回帰分析、分割法、直交配列までを網羅し、QC検定1級レベルの試験範囲をほぼカバーしている内容です。品質管理と実験計画法を独学で実践できるようにノウハウが基礎からしっかりと解説されている一冊です。
QC検定1級レベルなのでそこそこの難易度ですが、基礎から丁寧に説明されているので独学でも十分理解できる内容だと思います。例題の解法も具体的な手順がしっかりと記載されているため、実践しながら学べ非常に助かります。
この本は1993年に出版されていて少し古いなと感じるかもしれませんが、今でも非常に有用な内容です。実験計画法と品質管理の実践において非常に役立つ一冊です。実験計画法を学びたい方やQC検定を目指している方におすすめです!
実験計画法で使われる用語と意味
解説に入る前に、実験計画法で使用される用語とその意味について整理しておきましょう。
この記事で出てくる用語は以下の通りです。
| 用語 | 意味 |
|---|---|
| 特性 | 結果として得られる性質のこと。実験計画法では基本的に数値で表せされる定量的な品質データを示す。 |
| 因子 | 条件の変化によって特性値に影響をあたえられると考えられるもの。特に最適条件を知ることを目的として自らが設定する因子を制御因子という。 |
| 水準 | 実験にあたり因子を変動させる場合に代表地として選んだ値。 |
| 群間変動 | 群(水準)の違いによる特性値のばらつき、級間変動または水準間変動とも呼びます。 |
| 群内変動 | 同じ軍の中での特性値のばらつき。級内変動または水準内変動とも呼びます。 |
| 主効果 | 因子の水準を変えることによって特性値が変動する影響のこと |
| 相互作用 | 二つ以上の因子を扱う場合において相乗的あるいは相殺的に特性値が変動する影響のこと。 |
実験計画法【1】 実験の組み方
単一因子実験と要因実験
実験計画法の”実験の組み方”を説明するうえでまずは”単一因子実験”と”要因実験”について理解しましょう。
・単一因子実験とは??
たとえば、因子Aと因子Bの2つの最適な組み合わせを決定したい場合、①因子Bを固定して因子Aの最適水準を決定⇒②最適な因子Aで固定して因子Bを実験する。このように一度の実験で因子を1つずつ取り上げる実験方法を単一因子実験(一元配置実験)といいます。
しかし、単一因子実験では誤った結論を導き出すことがあります。
因子Aが3水準(A1,A2,A3)と因子Bが2水準(B1,B2)の場合を考えてみます。”真のデータ”は以下のグラフとします。実験手順を以下とする場合の結論はどうでしょうか?
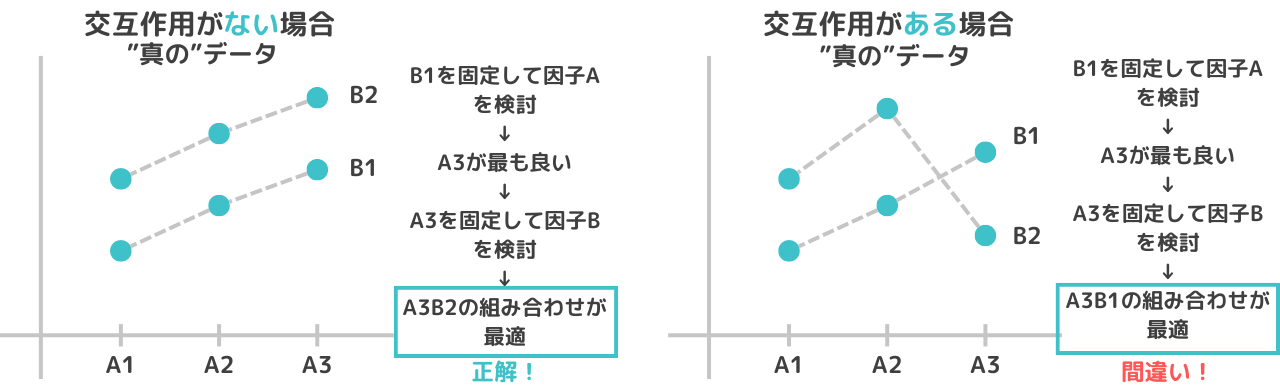
上の図から”交互作用がある場合”ではA2,B2の組み合わせが最も高い値を示すにも関わらず間違った結論を出してしまうことがわかります。
・要因実験とは??
問題とする因子を同時に取り上げ、因子の水準全ての組み合わせを実験する方法です。要因実験では交互作用がある場合でも正しく評価できます。相互作用がないとわかっている場合でも要因配置実験の方が得られるデータの精度の面で有利です。先ほどの単一因子実験と比べるとデータは以下のようになります。
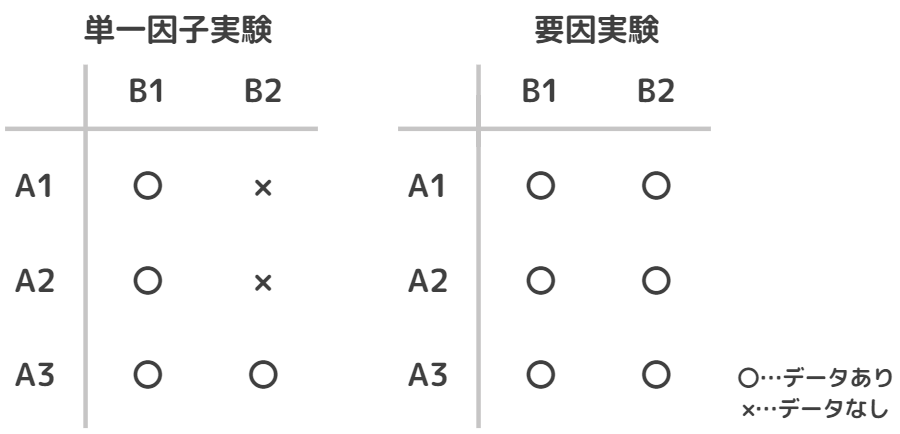
水準の組み合わせを総当たりで行う実験で、因子が二つの場合を2因子実験(二元配置実験)、三つ以上を多元配置実験といいます。
≫繰り返しのない二元配置分散分析
≫繰り返しのある二元配置分散分析
その他の実験方法|ラテン方格と直交表
単一因子実験、要因実験以外の実験方法について解説します。
ラテン方格とは??
3×3からなる方格に3種類の数字をどの行、どの列にも1回ずつ現れるように並べられた方格です。
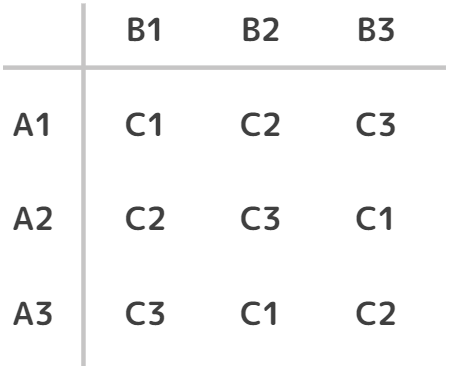
A1で行う実験にはB1,B2,B3,C1,C2,C3がいずれも1回ずつ入っています。この性質はA2,A3で行う実験でも同様です。すべての実験で因子の影響が平等に入っているため、これらの和または平均を比較することで、各因子の効果の推定値を得ることができます。
仮に3因子、3水準の要因実験をするとなると、3の3乗で27回の実験をすることになりますが、交互作用がない場合はこのように一部の実験で主効果を推定することが可能です。
直交表とは??
ラテン方格をもとに開発された実験方法が直交表です。直交表は実験計画法の一環として、多数の実験条件の組み合わせを効率的に選定するための実験方法です。直交表を使うことで、全ての組み合わせを試す必要がなく、一部の組み合わせで十分な情報を得ることができます(一部実施要因計画)。
たとえば、3因子、3水準すべてを実験しようと思うと33=27回の実験をする必要がありますが、L9(34)直交表を使えば9回で検証できます。
実験計画法【2】 実験の場の管理の考え方
実験には実験ごとのばらつき、”実験誤差”を完全に排除することはできません。そこで実験誤差は発生するものと認めて、積極的に実験誤差を制御し、管理するという考えのもと実験を行う必要があります。
フィッシャーの3原則
実験管理の基盤となった”フィッシャーの3原則”について簡単に説明します。実験計画法の祖であるR.A.フィッシャーは、科学的研究において信頼性の高いデータを収集するための三つの基本原則を提唱しました。
1. 反復の原則(Replication)

データのばらつきを小さくするため、可能な限り多くの実験を行います。例えば、異なる条件下で同じ実験を行うことで、偶然の誤差を最小限に抑えます。反復によってデータのばらつきや外れ値を評価しやすくなります。
具体例
農業の研究で、特定の肥料の効果を評価する際に、異なる地域や季節で繰り返し実験を行うことで、肥料の効果が一貫しているかを確認できます。このように、反復することで、得られたデータの信頼性が向上します。
2. 無作為化の原則(Randomization)

サンプリングや条件設定をランダムに行うことで、系統的な誤差を偶然誤差に変え、系統誤差の影響を最小化し、結果の信頼性を高めることができます。
具体例
例えば、医薬品の効果を調べる臨床試験では、被験者を無作為に治療群と対照群に分けます。これにより、各群における年齢や性別などの影響を均等にし、治療の効果を正確に評価することが可能です。
3. 局所管理の原則(Local Control)
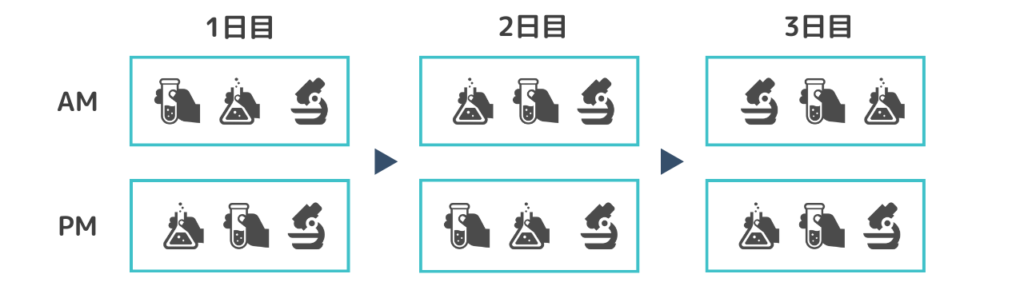
実験規模の拡大を抑えるため、実験をブロックに分けて管理することで、実験条件の均一化を図る方法です。ブロック内で条件を無作為に割り当てることで、ブロック間の変動を抑え、精度の高い結果を得ることができます。
具体例
農業試験で、異なる土壌条件の影響を最小限にするために、農地を小さな区画に分け、それぞれの区画内で肥料の種類をランダムに割り当てます。これにより、各区画内での土壌条件のばらつきを抑え、肥料の効果を正確に評価できます。
実験計画法【3】 実験データの解析の仕方
得られた実験データを客観的に判断するために仮説検定を用います。
たとえば、Aの水準間に差がないという仮説を立てて検定し、もしこの仮説が棄却された場合は、Aの水準間に違いがあると結論付けます。一方でこの仮説が棄却されない場合には、Aの水準間には有意な差はないと結論付けます。仮説の検定には分散分析を使って判定します。
≫一元配置分散分析を例題の手順
≫繰り返しのある二元配置分散分析の手順
≫繰り返しのない二元配置分散分析の手順
実験計画法に基づく実験計画フロー
最後に実験計画法を用いた実験の流れについて確認しましょう。実験は以下のフローで実施します。
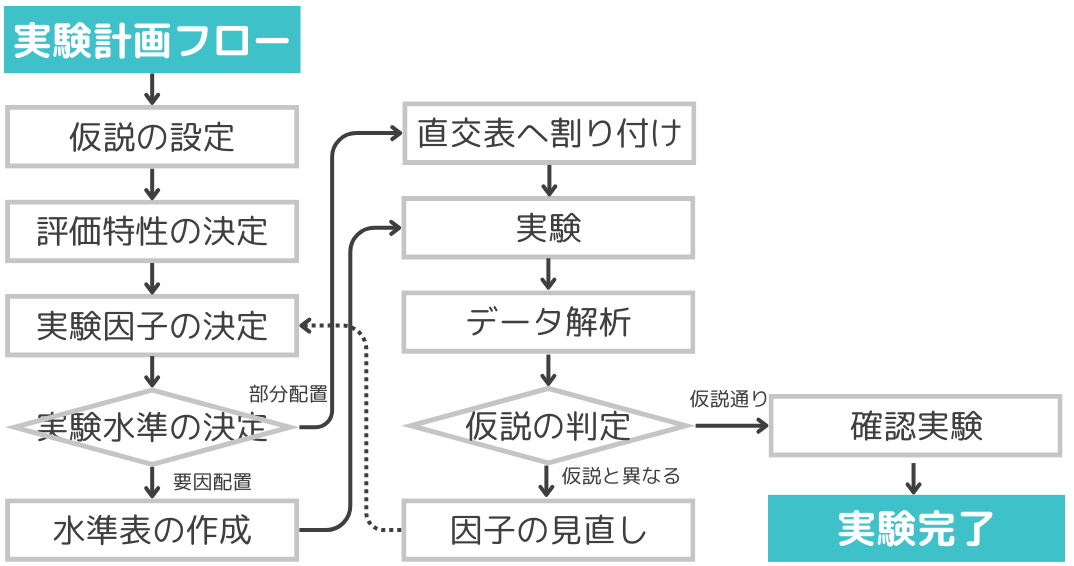
- 実験の目的と評価する項目、方法、目標を設定する。
- 目標を達成するための仮説を設定する。
- 仮説を立証するための検証方法、評価方法を決定する。
- 制御因子を設定する。タグチメソッドを使う場合は誤差因子、信号因子も設定する。
- 実験水準を作成し、要因配置実験、部分配置実験を選択する。
- 部分配置実験の場合は直交表に各因子を割り付け、水準を設定する。
- 実験する。
- 実験で得られたデータを分散分析などで解析する。
- 仮説通りの結果が得られた場合は再現性を評価する。
- 実験完了!
”Pythonを使った実験計画法”
『Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析』はPythonを用いたベイズ最適化を使った実験計画法を学ぶための入門書です。一般的にイメージされる直行表などの実験計画法とは違って、タイトル通りベイズ最適化に重きを置いています。
私はベイズ最適化と実験計画にPythonを取り入れたかったためこの本を購入しました。サンプルデータやサンプルコードが付いているので実践的に学びやすいですが、Python初心者には少し難しい内容かもしれません(私がそうでした。。)ですが、古典的実験計画法と異なるアプローチとサンプルコードはとても勉強になり、何度も読み返しています。解説も非常に丁寧でわかりやすく、行列などの基礎数学の補足解説もあり親切です。
Pythonを使って実験計画法に取り組みたい、ベイズ最適化の手法を知りたいという方におすすめの一冊です。


