”ウェルチのt検定”を例題でわかりやすく解説

ｔ検定を使うことで「2つのデータに差があるかどうか」を統計学的に判断することができます。
t検定には以下の種類があり、この記事では”ウェルチのt検定”の実施手順について解説します。

• 等分散を仮定した対応のないt検定（スチューデントのt検定）
• 等分散を仮定しない対応のないt検定（ウェルチのt検定）
• 対応のあるt検定

ウェルチのt検定とは

ウェルチのt検定は、2つのグループ（2群）の平均値を比較し、その差が統計的に有意かどうかを判断するための手法です。ウェルチのt検定はｐ値による有意差判定と母平均差分の信頼区間から構成されます。スチューデントのt検定と似ていますが、2つのグループの分散が異なる場合に適用されます。

ウェルチのt検定は以下条件に当てはまる場合に適用します。それ以外の場合は他のt検定を適用します。

• 2群のデータは対応のないデータであること
• ２つの母集団は正規分布に従っていること
• 2群のデータの分散が等しいとはいえないこと

ウェルチのt検定の手順をわかりやすく解説

以下ウェルチのt検定の実施手順を解説します。以降記載の”t検定”は”ウェルチのt検定”のことを意味します。

t検定手順1．仮説を立てる

1. 帰無仮説（H₀）：群1と群2の母平均値に”差がない”
2. 対立仮説（H₁）：以下のいずれかの仮説を設定
   • 群1の母平均は群2の母平均より”大きい”
   • 群1の母平均は群2の母平均より”小さい”
   • 群1の母平均と群2の母平均は”異なる”

t検定手順2．検定方法（両側検定or片側検定）を決める

　対立仮説によって自動的に決まります。

• 群1の母平均は群2の母平均より”大きい”　⇒　片側検定（右側検定）
• 群1の母平均は群2の母平均より”小さい”　⇒　片側検定（左側検定）
• 群1の母平均と群2の母平均は”異なる”　⇒　両側検定

t検定手順3．統計量（t値）を算出する

2群の平均値、標準偏差、サンプルサイズからt検定の統計量（t値）を計算します。

t検定手順4．ｐ値を算出、有意差判定

計算したt値と自由度を用いて、p値を算出します。
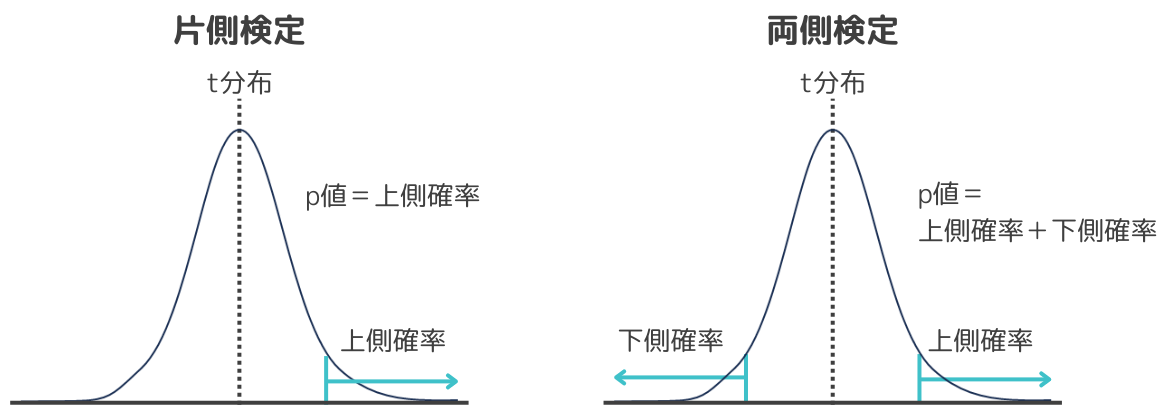
・片側検定のｐ値はt分布における検定統計量の上側確率
・両側検定のｐ値はt分布における検定統計量の上側確率の2倍。

ウェルチのt検定はスチューデントのt検定と異なり、自由度は以下の式で計算します。

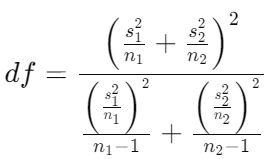
p値が事前に設定した有意水準（例えば0.05）の場合、
・p値<有意水準0.05　⇒　帰無仮説を棄却し対立仮説を採択 有意差がある
・p値≧有意水準0.05　⇒　対立仮説を採択できず、有意差があるといえない

t検定手順5．信頼区間を算出する

信頼区間は以下の式で求められます。

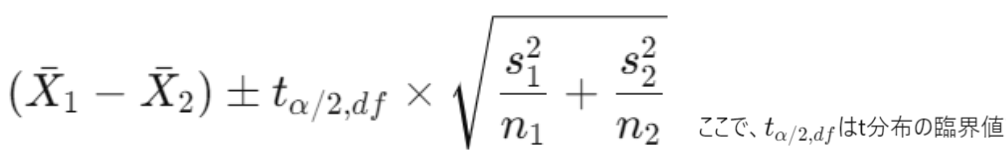
信頼区間を適用しての有意差検定を行う
・信頼区間が0をまたがらない　⇒　2群の母平均値は異なる
・信頼区間が0をまたがる　⇒　2群の母平均値は異なるといえない

【例題】ウェルチのt検定をやってみよう！

では具体的な例題を使って、t検定を実際に行ってみましょう。

1．仮説を立てる
　・帰無仮説：グループAとグループBの平均得点に差はない。
　・対立仮説：グループAとグループBの平均得点に差がある。

2．検定方法
グループAとグループBの平均得点は”異なる”なので”両側検定”

3．統計量を算出する
・各グループの平均値を計算

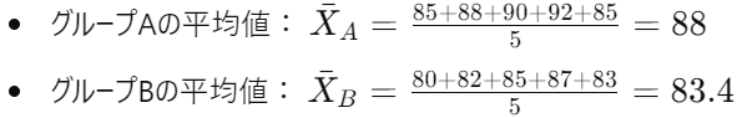
・各グループの標準偏差を計算

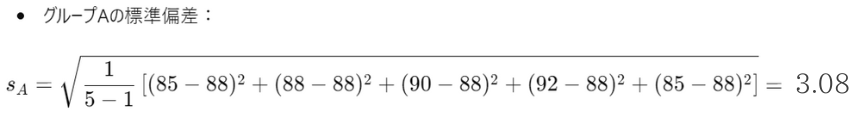
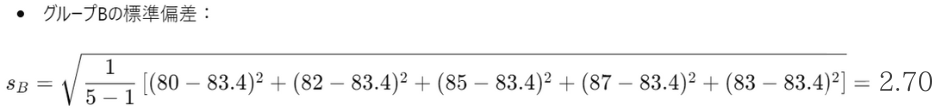
・t値を計算

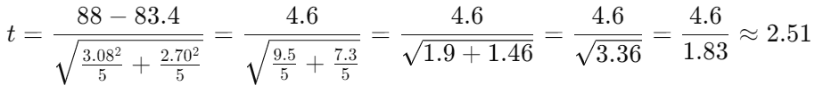
4．p値を算出、有意差判定
自由度を以下の式で計算します。

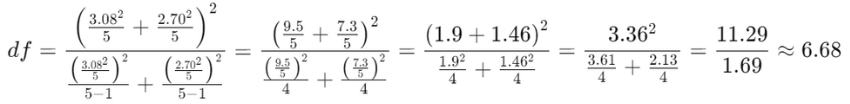
t分布表を使って、t値2.51に対応するp値を求めます。p値が”0.0459”でした。これは有意水準0.05より小さいので、帰無仮説を棄却し対立仮説を採択 有意差があるといえます。

5．信頼区間を算出
95%信頼区間を計算します。

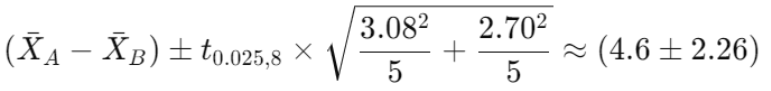
信頼区間は (2.34, 6.86) となり、0を含まないため、2つのグループの平均値に有意な差があると言えます。

【関連記事】
≫スチューデントのt検定
≫対応のあるt検定