統計学では、データから正確な意思決定を行うためにT検定やF検定を使います。しかし、どのような分析をしたいかによって使用する検定方法を選択する必要があります。
この記事ではT検定とF検定の具体例を使って2つの検定方法の違いと、どちらの検定方法を採用したらよいか解説します。
【この記事でわかること】
・T検定、F検定のやり方
・T検定、F検定を使用する例題
F検定とは?
F検定は複数のグループ間での分散(データのばらつき)の違いを比較するための検定です。F検定は分布を用いた検定の総称で、特に一元配置分散分析、二元配置分散分析などの分散分析(ANOVA: Analysis of Variance)で頻繁に使用されます。
F検定が使用される場面
F検定は以下のような場面で使用されます
- 分散分析(ANOVA):複数のグループの平均値を比較するときに、まず各グループの分散が等しいかを確認するために使用
- モデルの適合度検定:回帰分析などのモデルにおいて、モデルがデータにどれだけ適合しているかを評価するために使用
- 2つの標本の分散比較:2つの標本が同じ母分散を持つかどうかを比較するために使用
F検定の’メリット’と’デメリット’は?
メリット
・複数のグループ間で分散の違いを比較できる。
・分散分析(ANOVA)での使用で複数の平均値の比較が可能になる。
デメリット
・正規分布に従わないデータには適さない。
・異常値に敏感でありデータのばらつきに影響を受けやすい。
F検定の計算方法と手順概要
F検定の計算は以下の手順で行います。
【データ分析ツールのt検定手順】
1.分散の計算:各グループの分散を計算
2.F値の計算:分散の比を計算します。通常、より大きい分散を分子に、小さい分散を分母にして計算します。F値 = 分子の分散 / 分母の分散
3.p値を求める:計算されたF値を使い、対応する自由度(分子自由度と分母自由度)に基づいてF分布を参照し、p値を求める。
4.結論:p値が所定の有意水準(通常は0.05)以下であれば、分散に有意な差があると結論付けます。
F検定の具体例

【例:おいしいカレーを作るために作り方(一元配置分散分析)】
煮込み時間を10分、20分、30分と変えてカレーを作り、カレーの美味しさを1~10の10段階評価で点数付けをしてみます。各水準をN回実験し、得られた評価結果を分散分析で水準間に有意差があるか検証します。
T検定とは?
t検定は2つのグループ間の平均値の差が統計的に有意であるかどうかを判断するための手法です。この検定はサンプルの平均値が母集団の平均値と異なるかどうか、または2つの独立したサンプルの平均値が異なるかどうかを調べるときに使用されます。t検定は、データが正規分布に従うという前提のもとで行われます。
T検定が使用される場面
t検定には種類があり以下のような場面で使い分けされます
- 対応のない2標本T検定:2つの独立したグループの平均値を比較する際に使用されます。
- 対応のある2標本T検定:同じ対象に対して2つの異なる条件下での測定値を比較する際に使用されます。
▶Excelでt検定のやり方を種類ごとに解説
▶t検定 どの種類を使えばよい?
t検定の’メリット’と’デメリット’は?
メリット
・平均値の差を直接比較できる。
・実施が比較的簡単であり、広く利用されている。
デメリット
・データが正規分布に従う必要がある。
・サンプルサイズが小さい場合、検出力が低くなることがある。
T検定の計算方法と手順概要
t検定の計算は以下の手順で行います。
【データ分析ツールのt検定手順】
1.平均値と分散の計算:各グループの平均値と分散を計算します。
2.標準誤差の計算:グループ間の平均値の差の標準誤差を計算します。
3.t値の計算:t値を計算します。t値 = (平均値の差) / (標準誤差)
4.p値を求める:t値を使って対応する自由度に基づいてt分布を参照し、p値を求める。
5.結論:p値が有意水準(通常は0.05)以下であれば、平均値に有意な差があると結論付ける。
T検定の具体例
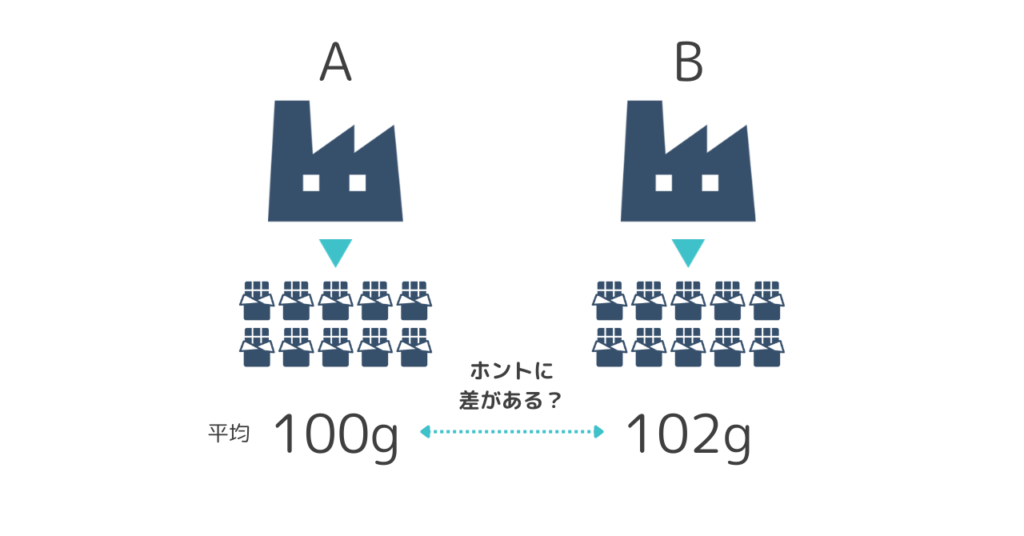
【例:チョコレート工場2拠点の製品検査】
とあるチョコレートを製造している工場が2拠点あります。それぞれ製品検査のため無作為に製品を10個選び、重量を測定したところ平均値は、工場Aは100g、工場Bは102gでした。工場間で同一製品が作られているか検証する。
F検定とt検定の比較
使用する場面の違い
F検定
・複数のグループの分散を比較するときに使用する。
(例 3つ以上の異なるグループのパフォーマンスのばらつきを比較する場合)
T検定
・2つのグループの平均値を比較するときに使用する。つまり、サンプルが2つの場合に限定されます。
(例 新薬の効果をプラセボと比較する場合や、治療前後のデータを比較する場合)
前提条件の違い
F検定
・分散が正規分布に従うこと。
・各グループのデータが独立していること。
・データの同質性(分散の等質性)を仮定する。
T検定
・データが正規分布に従うこと。
・対応のない2標本t検定では、2つのサンプルが独立していること
・対応のある2標本t検定では、同じ対象に対して繰り返し測定が行われること
結果の解釈の違い
F検定
・F値が大きいほど、グループ間の分散が異なることを示す。
・p値が有意水準以下であれば、分散の違いが有意であると判断する。
・分散の違いを明確にするため、後続の多重比較検定が必要になることが多い。
T検定
・t値が大きいほど、グループ間の平均値が異なることを示す。
・p値が有意水準以下であれば、平均値の違いが有意であると判断する。
・グループ間の平均値の差が統計的に有意であるかどうかを直接示す。
F検定とT検定どちらを選ぶべきか
- グループの数:
- グループが2つの場合 ⇒ t検定
- グループが3つ以上の場合 ⇒ F検定(ANOVA)
- 比較の対象:
- 平均値の比較 ⇒ t検定
- 分散の比較 ⇒ F検定
- データの性質:
- データが正規分布に従う場合 ⇒ どちらの検定も使用可能
- 正規分布に従わない場合 ⇒ ノンパラメトリック検定の検討が必要


