統計学は、データから意味ある情報を引き出し、より良い意思決定を支援する強力なツールです。その中心的な概念のひとつが「仮説検定」です。この記事では、仮説検定の基本を初心者にもわかりやすく解説します。
仮説検定とは?
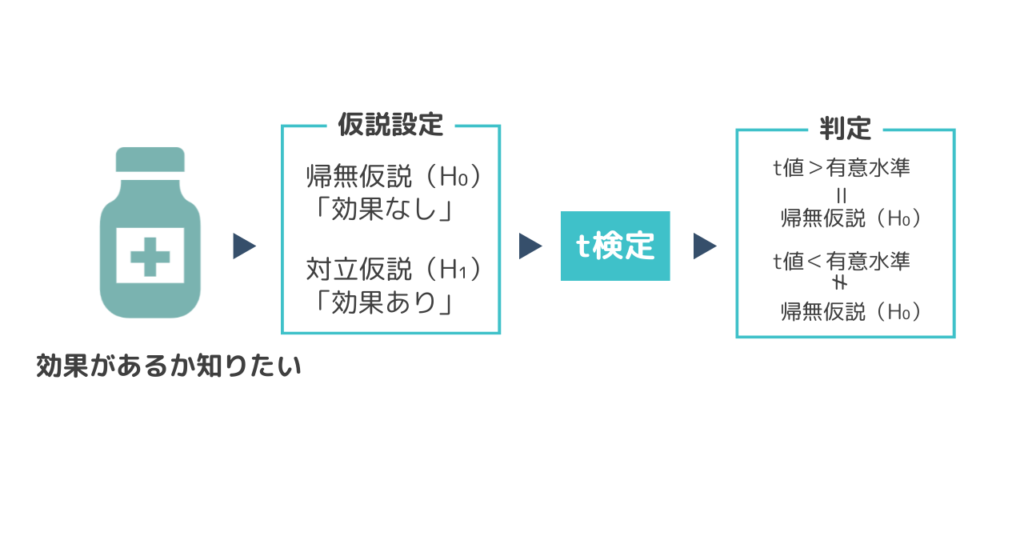
仮説検定は簡単に言うと「ある考えが統計的に正しいかどうかをチェックする方法」です。
仮説検定で大事なのが、帰無仮説(H₀)と対立仮説(H₁)の設定。帰無仮説は「変化なし」や「効果なし」といった状態を示し、対立仮説は「何かしらの効果がある」ということを示します。データ分析の結果、成績が有意に向上していることが帰無仮説は棄却し、対立仮説を採用します。
ではどのようにして帰無仮説(H₀)と対立仮説(H₁)を判断するのでしょうか。仮説検定では、有意水準によって判断基準を設定します。計算した結果が、有意水準よりも小さい場合は帰無仮説(H₀)は間違っている、つまり対立仮説(H₁)が正しいと判断できます。反対に計算結果が有意水準よりも大きい場合、帰無仮説(H₀)が正しいと判断できます。
有意水準とP値
仮説検定では、帰無仮説と対立仮説を判断する基準として「有意水準」というものを設定します。
有意水準はα(アルファ)と呼ばれることもあり、これは帰無仮説を誤って棄却するリスクのことです。一般的には5%(α=0.05)や1%(α=0.01)が使われます。
そして、仮説検定には有意水準と同じくらい重要なP値というものがあります。P値は「帰無仮説が正しいとしたときに、私たちのデータがどれくらい珍しいか」を示します。P値が小さいほど、帰無仮説を棄却する根拠が強くなります。
第一種と第二種の誤りとは
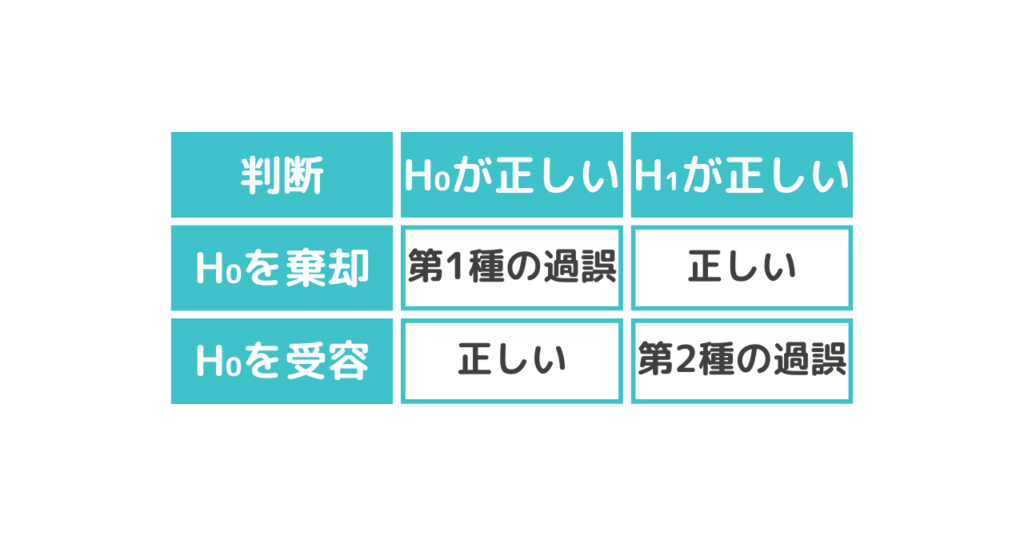
仮説検定には、誤りのリスクが伴います。第一種の誤り(第一種の過誤)は、「帰無仮説が真実であるにもかかわらず、誤って棄却すること」です。第二種の誤り(第二種の過誤)は、「帰無仮説が偽であるにもかかわらず、棄却されないこと」です。
仮説検定の使用例
例えば、学校で新しい教育プログラムを始めたとしましょう。このプログラムが学生の数学の成績にどのような影響を与えるかを知りたいと思います。
ここでの帰無仮説(H₀)は「新しいプログラムは成績に影響しない」とし、対立仮説(H₁)は「新しいプログラムは成績を向上させる」と設定します。
この仮説を検証するために、学校はプログラム導入前後の学生の数学の成績を比較します。もし、データ分析の結果、成績が有意に向上していることが示されれば(つまり、P値が非常に小さい場合)、帰無仮説は棄却され、新しいプログラムが効果的であると結論づけることができます。
まとめ
仮説検定は、データを使った意思決定に欠かせないツールです。少し難しく感じるかもしれませんが、基本を理解すれば、データの世界がもっと身近に感じられるはずです。統計学、面白いですよ!


