相関分析は、2つ以上の変数間の関係性を測定するための統計手法で、相関係数を見れば変数間の関係の強さと方向がわかります。相関係数はエクセルの分析ツールや関数を使うことで、簡単に求めることができます。
この記事では相関係数をExcel分析ツールと関数を使って計算する手順、結果の見方について解説します。
【この記事でわかること】
・エクセル「分析ツール」と関数を使った相関係数の計算方法
・相関係数の見方と意味
エクセルの分析ツールを使った相関分析の手順
相関分析は”勤続年数と年収”、”広告費と売上”など、2以上の変数間の関係性を分析したいときに使用します。
今回の相関分析は”気温”と”アイスクリームの売り上げ”に関するデータを使用して説明します。データはchatGPTを使って生成した仮想データです。
まず、エクセルの分析ツールを使って相関分析を行う手順を解説します。
分析ツールの有効化
エクセルで回帰分析を行うためには、「分析ツール」を有効にする必要があります。このツールはデフォルトでは有効化されていないことが多いので、まずは「データ分析」ツールを有効化する必要があります。
データ分析ツールの有効化手順
- Excelを開き、上部にある「ファイル」タブをクリックします。
- メニューの一番下にある「オプション」を選択します。
- 左側のメニューから「アドイン」カテゴリを選択し、「分析ツール」を見つけます。
- 下部の「管理」ボックスで「Excelアドイン」を選択し、「設定」をクリックします。
- 表示されるリストから「分析ツール」にチェックを入れ、「OK」をクリックします。
これで、分析ツールが使用可能になります。
具体例で相関分析の手順を解説
次に、具体的な相関分析の手順を説明します。
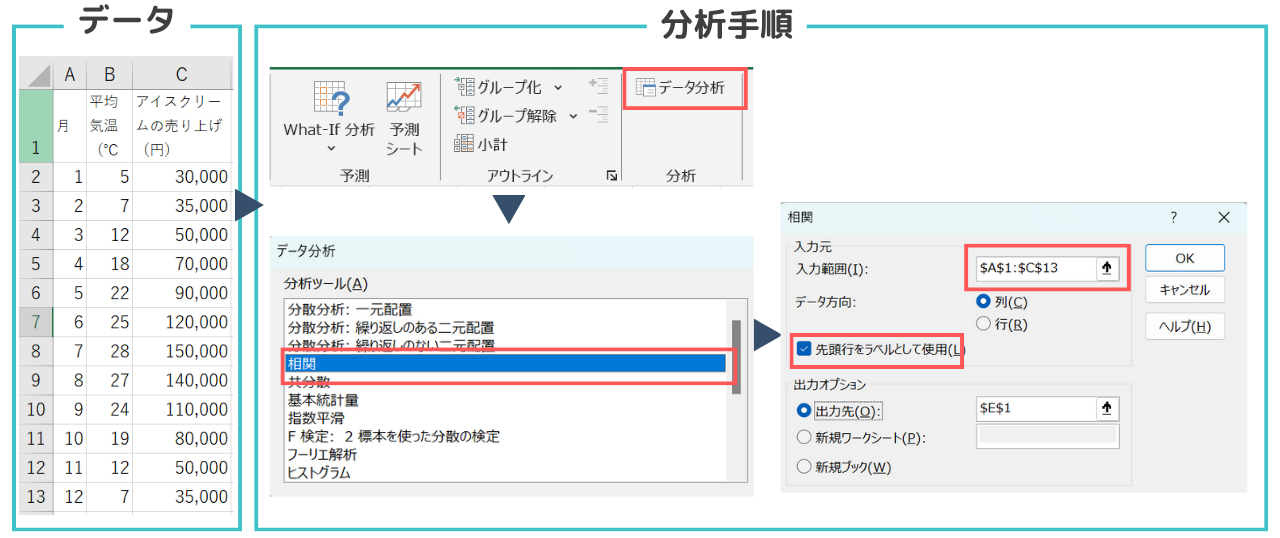
単回帰分析の手順
- データ分析ツールを選択:Excelの「データ」タブに移動し、右端にある「データ分析」を選択
- 相関を選択:表示されるリストから「相関」を選択
- 入力範囲の指定:
- 入力範囲:相関を計算したいデータの範囲を選択します。(例:$A$1:$C$13)
- ラベル:データの最初の行にラベルが含まれている場合は、「ラベル」にチェックを入れます。
- 出力範囲:分析結果を表示するセル範囲を指定します。(例:$E$1)
- OKをクリック:設定が完了したら、「OK」ボタンをクリック。エクセルが相関分析を実行し、指定したセル範囲に結果を出力します。
相関分析の結果の見方、相関係数の解釈
ここで相関分析の結果の見方、解釈について説明します。相関係数は、2つ以上の変数間の関係の強さと方向を示す指標であり、相関係数の値は -1 から 1 の範囲で変動し、以下のように解釈されます。
変数間の関係の方向
相関係数の値は -1 から 1 の範囲で変動し、変数間の関係の方向性を表します。
- +1:完全な正の相関。1つの変数が増加するにつれて、もう1つの変数も一定の割合で増加。
- 0:相関なし。2つの変数の間に線形の関係はなし。
- -1:完全な負の相関。1つの変数が増加するにつれて、もう1つの変数は一定の割合で減少。
変数間の関係の強さ
相関係数の大きさ(絶対値)が大きいほど、2つの変数間の関係が強いことを示します。一般的には以下の様に解釈する場合が多いです。
- 0.9~1:非常に強い正の相関
- 0.7~0.9:強い正の相関
- 0.5~0.7:中程度の正の相関
- 0.3~0.5:弱い正の相関
- 0~0.3:ほとんど相関なし
- -0.3~0:弱い負の相関
- -0.5~-0.3:中程度の負の相関
- -0.7~-0.5:強い負の相関
- -1~-0.7:非常に強い負の相関
例題の相関分析結果
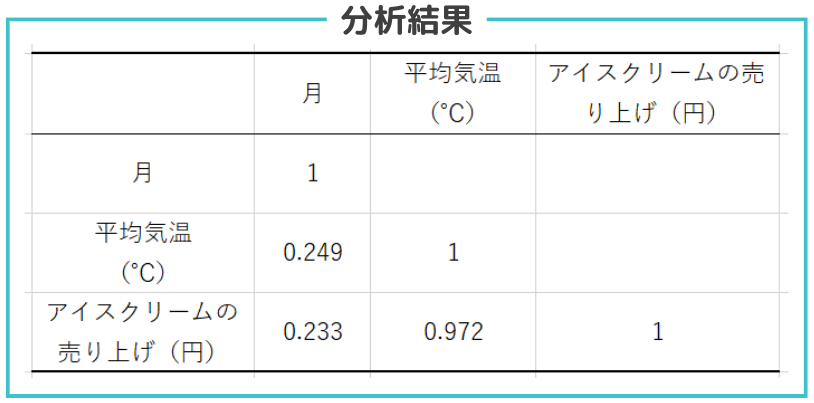
- 月と平均気温、アイスクリームの売り上げの相関係数
月と平均気温の相関係数は”0.249”、月とアイスクリームの売り上げの相関係数は”0.233”でありどちらもほとんど相関関係がないことがわかります。 - 平均気温とアイスクリームの売り上げの相関係数
平均気温とアイスクリームの売り上げの相関係数は”0.972”と非常に強い正の相関関係であることがわかりました。つまり、平均気温が高くなるにつれアイスクリームの売り上げが上昇すると言えます。
季節と気温が相関していそうだから月と気温も相関関係にあるのでは?
結果を見て「夏は気温が高く冬は気温が低いので月と気温は相関性がありそう」と疑問に思った人もいるかもしれません。先ほどのデータを見ると7月の平均気温がピークに1月、12月にかけて減少する非線形(直線ではない形状)であることがわかります。相関分析は線形関係(直線的な関係)の分析に適した方法です。したがって、月が増すと気温が上がるとは言えず、相関関係はないという結果になります。
エクセルの関数を使って相関係数を計算する場合
分析ツールを使う以外に、関数を使っても相関分析を行うことができます。ここでは、代表的な関数である CORREL 関数と PEARSON 関数の使用方法について説明します。
CORREL関数の使用方法CORREL 関数は、2つの変数間の相関係数を計算するための関数です。相関係数は、-1から1の範囲の値を取り、2つの変数の間の関係の強さと方向を示します
- データを準備:エクセルに”気温”と”アイスクリームの売り上げ”のデータをB1~C13に準備
- 関数を入力:
- 気温のデータ範囲が
B2:B13、アイスクリームの売り上げがC2:C13に入力されていると仮定します。
-
CORREL関数を入力します。=CORREL(B2:B13, C2:C13)
- 気温のデータ範囲が
- 結果の確認:Enterキーを押すと、指定した2つのデータ範囲の相関係数が表示されます
PEARSON関数の使用方法PEARSON 関数も、2つの変数間のピアソンの相関係数を計算するための関数です。実際には CORREL 関数と同じ結果を返しますが、名前が異なるだけです。使用方法もCORREL関数と同じです。
相関分析をするときに注意すべきポイント
相関関係と因果関係は違う
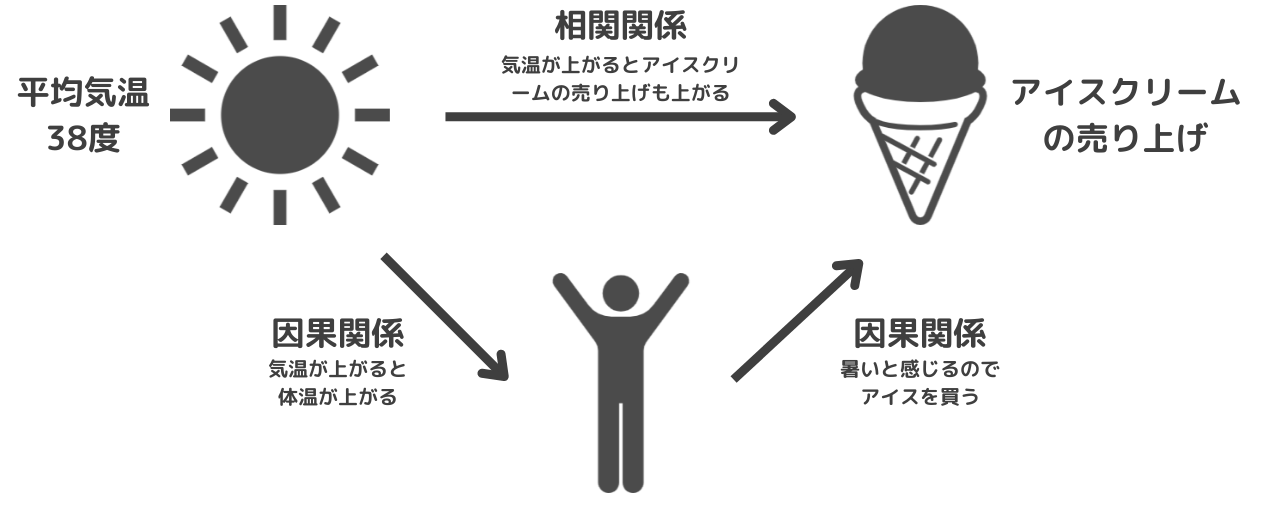
相関関係と因果関係は、データ分析においてよく混同される概念ですが、それぞれ異なる意味を持ちます。
相関関係
2つの変数が一緒に変動する傾向があることを意味します。しかし、相関関係は必ずしも一方が他方を引き起こす(因果関係がある)ことを意味しません。
- 例1:アイスクリームの売上と気温の間に強い正の相関があるとします。気温が上がるとアイスクリームの売上も増えますが、これは気温がアイスクリームの売上を引き起こしているとは限りません。実際には、暑い天候が人々にアイスクリームを買いたくさせるという共通の要因が存在します。
- 例2:広告費と売上に相関関係がある場合、広告費を増やすと売上も増える傾向が見られるかもしれませんが、これも因果関係を示すものではありません。他の要因(例えば、季節要因や市場のトレンド)が関係している可能性もあります。
因果関係
一方の変数が他方の変数を直接引き起こす関係(原因)です。因果関係を証明するには、相関関係だけでは不十分であり、実験や詳細な分析が必要です。
- 例1:科学実験において、特定の薬を投与したグループと投与しなかったグループの比較を行うことで、その薬が健康改善に因果的な効果を持つかどうかを検証する。
- 例2:ビジネスにおいて、特定のマーケティングキャンペーンを実施した地域としなかった地域の売上データを比較することで、そのキャンペーンが売上増加に因果的な影響を与えるかどうかを確認する。
外れ値の影響を受けやすい
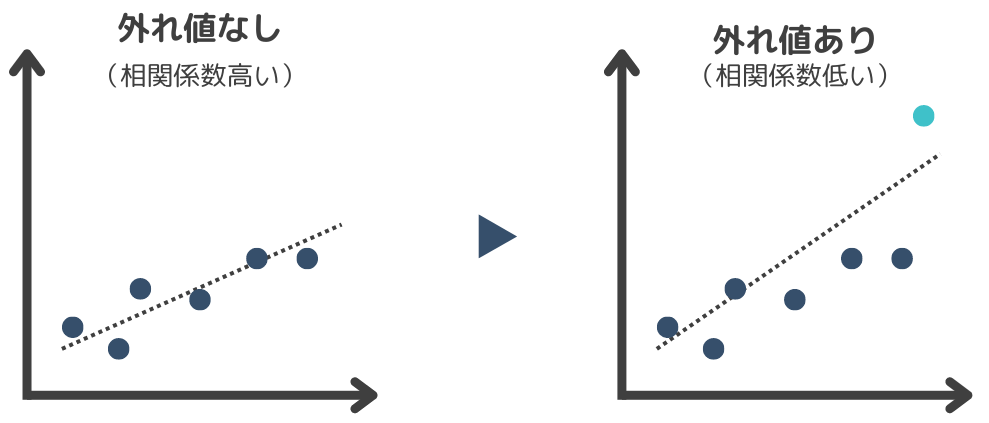
相関分析は何らかのエラーによって生じた外れ値におおきく影響されます。
相関分析を行う際には外れ値を考慮して分析を進める必要がありますが、外れ値は必ずしも悪いというわけではありません。外れ値が必然な値であれば”新たな知見”である可能性があります。外れ値がエラーなどによる偶然のものなのか、特異的な値を示す必然のものなのかは慎重に判断する必要があります。
非線形を示すデータには対応できない
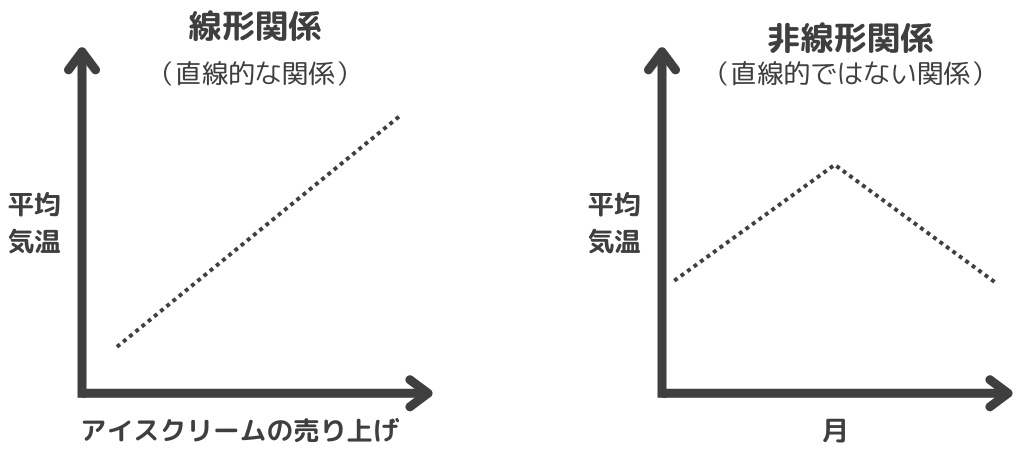
相関分析が対応できるのは線形関係(直線的な関係)であり、非線形(直線ではない関係性)を捕捉することは困難です。相関分析の結果の数値だけを見て判断せず、散布図を描画したり、変数間の特性を考慮して判断しましょう。



