”繰り返しのある二元配置分散分析”を例題でわかりやすく解説

分散分析（ANOVA：analysis of variance）は、3群以上の平均値の有意差を調べる場合に使う分析手法です。
分散分析は全体的な平均値の相違を調べる方法であり、どの群間に有意差があるかは把握できません。そのため、分散分析で相違が認められた場合は、どこの群間に有意差があるか多重比較法によって検証する必要があります。

分散分析には”一元配置分散分析”と”二元配置分散分析（繰り返し有り、無し）”の2種類があり、この記事では”繰り返しのある二元配置分散分析”について解説します。

二元配置分散分析とは

二元配置分散分析（Two-Way ANOVA）は、2つの独立変数（因子）が従属変数に与える影響を同時に評価するための統計手法です。この分析は、各因子が従属変数に与える個別の影響（主効果）と、それらの因子が組み合わさったときの相互作用の影響（交互作用効果）を調べることができます。

二元配置分散分析は、因子Aの主効果、因子Bの主効果、交互作用（因子Aと因子Bの組み合わせによる効果）、誤差の大きく4つに分けて計算し、計算を行うと以下のような分散分析表が作成できます。

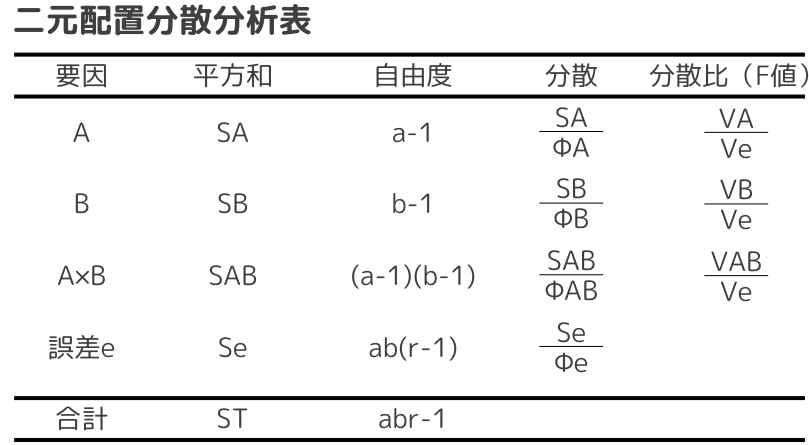
表を見てわかる通り、分散比（F値）は因子A、因子B、交互作用のそれぞれが誤差の分散（Ve）に対してどの程度大きいかを表しています。つまり、Veに対して主効果または相互作用が大きければ、それらの影響が大きいことを表しています。

繰り返しのある二元配置分散分析の手順をわかりやすく解説

”二元配置分散分析”手順1．仮説を立てる

1. 主効果Aの仮説：
   • 帰無仮説（H_0A）：独立変数Aの効果はない。
   • 対立仮説（H_1A）：独立変数Aの効果はある。
2. 主効果Bの仮説：
   • 帰無仮説（H_0B​）：独立変数Bの効果はない。
   • 対立仮説（H_1B​）：独立変数Bの効果はある。
3. 交互作用効果の仮説：
   • 帰無仮説（H_0AB）：独立変数AとBの間に交互作用効果はない。
   • 対立仮説（H_1AB​）：独立変数AとBの間に交互作用効果がある。

”二元配置分散分析”手順2．検定方法（両側検定or片側検定）を決める

通常、二元配置分散分析では”両側検定”を使用します。
（独立変数がどちらの方向にも影響を与える可能性があるため）

”二元配置分散分析”手順3．分散分析表を算出する

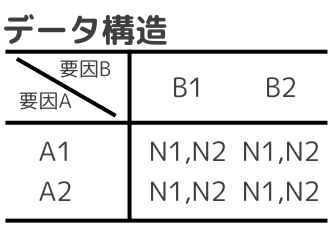
1. 平均：各水準、各要因、全体の平均を計算
   • 水準1平均（要因A×要因Bの水準） = 水準1データ合計 / 水準1サンプル数　（※同様に全水準実施）
   • 要因A1平均 = 要因A1データ合計 / 要因A1サンプル数
   • 要因A2平均 = 要因A2データ合計 / 要因A2サンプル数
   • 要因B1平均 = 要因B1データ合計 / 要因B1サンプル数
   • 要因B2平均 = 要因B2データ合計 / 要因B2サンプル数
   • 全体平均 = 全データ合計 / 全サンプル数
2. 要因Aの変動（SA）：要因Aによる変動を計算
   • SA = 要因Aサンプル数×((要因A1平均 – 全体平均)^2 + (要因A2平均 – 全体平均)^2)
3. 要因Bの変動（SB）：要因Bによる変動を計算
   • SB = 要因Bサンプル数×((要因B1平均 – 全体平均)^2 + (要因B2平均 – 全体平均)^2)
4. 交互作用効果の変動（SAB）：要因Aと要因Bの交互作用による変動を計算
   • SAB = 水準nサンプル数×∑(水準n – 全体平均)^2 – SA -SB
5. 誤差変動（Se）：残りの変動を誤差変動として計算
   • Se = ∑水準n平方和
6. 自由度（Φ）：各変動の自由度を計算
   • 要因Aの自由度（ΦA） = 要因Aのサンプル数 – 1
   • 要因Bの自由度（ΦB） = 要因Bのサンプル数 – 1
   • 交互作用の自由度（ΦAB） = ΦA × ΦB
   • 全体の自由度（ΦT） = 全サンプル数 – 1
   • 誤差の自由度（Φe） = ΦT – ΦA – ΦB – ΦAB
7. 分散（V）：各変動を対応する自由度で割る
   • 要因Aの分散（VA） = SA / ΦA
   • 要因Bの分散（VB） = SB / ΦB
   • 交互作用効果の分散（VAB） = SAB / ΦAB
   • 誤差の分散（Ve） = Se / Φe
8. F値：各平均平方を誤差の平均平方で割る
   • 要因AのF値（FA） = VA / Ve
   • 要因BのF値（FB） = VA / Ve
   • 交互作用効果のF値（FAB） = VAB / Ve

”二元配置分散分析”手順4．p値を算出、有意差判定

F値と対応する自由度を用いてp値を算出します（ｐ値はＦ分布における分散比の上側確率）。
p値が事前に設定した有意水準（例えば0.05）の場合、
・p値<有意水準0.05　⇒　帰無仮説を棄却し対立仮説を採択。各群の母平均は異なるといえる。
・p値≧有意水準0.05　⇒　対立仮説を採択できず、各群の母平均は異なるといえない。

【例題】繰り返しのある二元配置分散分析をやってみよう！

具体的な例題を使って、二元配置分散分析を実際に行ってみましょう。

1．仮説を立てる
　【主効果Aの仮説】
　　・帰無仮説（H_0A）：性別の効果はない。
　　・対立仮説（H_0A）：性別の効果はある。
　【主効果Bの仮説】
　　・帰無仮説（H_0B​）：教育方法の効果はない。
　　・対立仮説（H_1B​）：教育方法の効果はある。
　【交互作用効果の仮説】
　　・帰無仮説（H_0AB）：教育方法と性別の間に交互作用効果はない。
　　・対立仮説（H_1AB​）：教育方法と性別の間に交互作用効果はある。

2．検定方法を決める
両側検定を使用する。

3．分散分析表を作成する

4．p値を算出、有意差判定
F値と対応する自由度を用いて、F分布表からp値を算出します。
要因Aのp値：0.03、要因Bのp値：0.137、交互作用：0.690

・要因Aのp値<有意水準0.05　⇒　帰無仮説を棄却し対立仮説を採択。性別の効果はあるといえる。
・要因Bのp値≧有意水準0.05　⇒　対立仮説を採択できず、教育方法の効果はあるとはいえない。
・交互作用のp値≧有意水準0.05　⇒　対立仮説を採択できず、相互作用の効果はあるとはいえない。

---