母集団の分布が正規分布に従うことを仮定しない検定法であるノンパラメトリック検定にはいくつかの種類があります。この記事では、データが”2群比較”かつ”対応のある”場合に使用する、ウイルコクソンの符号順位和検定について解説します。
ウイルコクソンの符号順位和検定とは
2つの関連したグループ(対応のあるデータ)間の中央値に有意差があるかどうかを検定するノンパラメトリック手法です。データが正規分布していない場合、サンプルサイズが小さい場合に特に適しています。データの符号と順位に基づいて計算されます。
”ウイルコクソンの符号順位和検定”と”ウイルコクソンの順位和検定(U検定)”の違い
どちらもノンパラメトリック検定ですが、データの特性によって使い分けます。ウイルコクソンの符号順位和検定は”対応あり”、ウイルコクソンの順位和検定は”対応なし”のデータに適用します。
対応あり:関連する2つのグループ(たとえば、同じ被験者の投薬前後の測定値を比較する場合)
対応なし:2つの独立したグループ(たとえば、異なるコーヒーの味を比較する場合)
ウイルコクソンの符号順位和検定の計算手順
以下ウイルコクソンの符号順位和検定の実施手順を解説します。
【1】仮説を立てる
- 帰無仮説(H0):群1と群2の2つ群の母集団の順位平均値は”同じ”
- 対立仮説(H1):以下のいずれかの仮説を設定
- 群1の母集団順位平均値は群2の母集団順位平均値より”大きい”
- 群1の母集団順位平均値は群2の母集団順位平均値より”小さい”
- 群1と群2の2群の母集団順位平均値は”異なる”
【2】両側検定、片側検定を決める
対立仮説によって自動的に決まります。
- 群1の母集団順位平均値は群2の母集団順位平均値より”大きい” ⇒ 片側検定(右側検定)
- 群1の母集団順位平均値は群2の母集団順位平均値より”小さい” ⇒ 片側検定(左側検定)
- 群1と群2の2群の母集団順位平均値は”異なる” ⇒ 両側検定
【3】検定統計量を算出
- 差の計算:2つの関連する測定値の差を計算
- 差の符号と絶対値の計算:差の符号を記録し、差の絶対値を計算
- 差の絶対値の順位付け:絶対値を昇順に並べ順位を付ける(同じ絶対値には平均の順位を割り当てる)。
- 符号付き順位の合計:正の差の符号付き順位の合計(W+)と負の差の符号付き順位の合計(W-)を計算。
- 検定統計量の計算:統計量WはW+またはW-の小さい方の値。
【4】p値を算出
- 2群のサンプルサイズが25以下 ⇒ サインランク検定表適用
- 2群のサンプルサイズが25以上 ⇒ z分布適用
【5】有意差判定
- p値<有意水準0.05 ⇒ 帰無仮説を棄却し対立仮説を採択。2群の順位平均値に有意差があるといえる
- p値≧有意水準0.05 ⇒ 対立仮説を採択できず、2群の順位平均値に有意差があるといえない
【例題】ウイルコクソンの符号順位和検定をやってみよう!
では具体的な例題を使って、ウイルコクソンの符号順位和検定を実際に行ってみましょう。
例題:パン屋の秘密のスパイス入りレシピの比較
あるパン屋さんが、新しいレシピ(秘密のスパイス入り)を導入し、従来のレシピと比較して味の改善を評価しようとしました。パン屋のオーナーは、家族とスタッフ(計7人)に従来のレシピと新しいレシピの両方を試食してもらい、それぞれの味を10点満点で評価してもらいました。その結果を基に、どちらのレシピが好まれるかを検定します。
| 試食者 | 従来のレシピ | 新しいレシピ |
| A | 6 | 8 |
| B | 7 | 7 |
| C | 8 | 9 |
| D | 5 | 6 |
| E | 6 | 8 |
| F | 4 | 7 |
| G | 7 | 9 |
【1】仮説を立てる
・帰無仮説:従来のレシピと新しいレシピの2群の母集団の順位平均値は”同じ”
・対立仮説:従来のレシピと新しいレシピの2群の母集団順位平均値は”異なる”
【2】検定方法
従来のレシピと新しいレシピの2群の母集団順位平均値は”異なる”なので”両側検定”
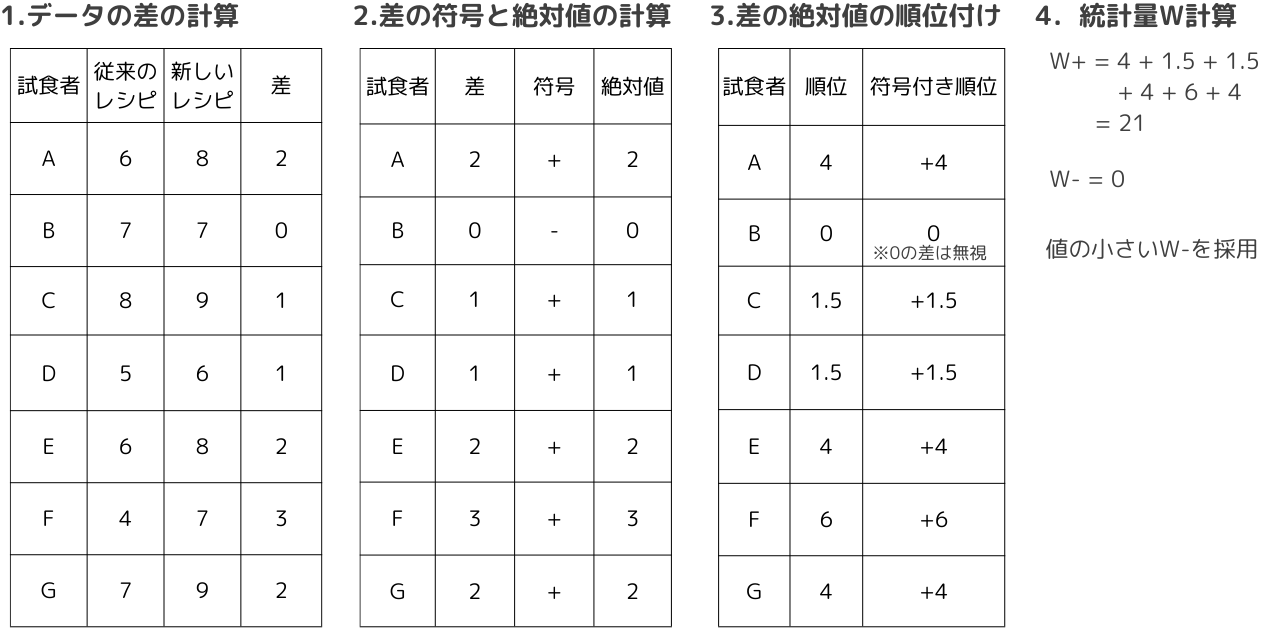
【3】統計量を算出
- 差の計算:2つの関連する測定値の差を計算
- 差の符号と絶対値の計算:差の符号を記録し、差の絶対値を計算
- 差の絶対値の順位付け:絶対値を昇順に並べ順位を付ける(同じ絶対値には平均の順位を割り当てる)。
- 検定統計量の計算:正の差の符号付き順位の合計(W+)と負の差の符号付き順位の合計(W-)を計算。W+またはW-の小さい方の値を統計量として採用。
【4】p値を算出
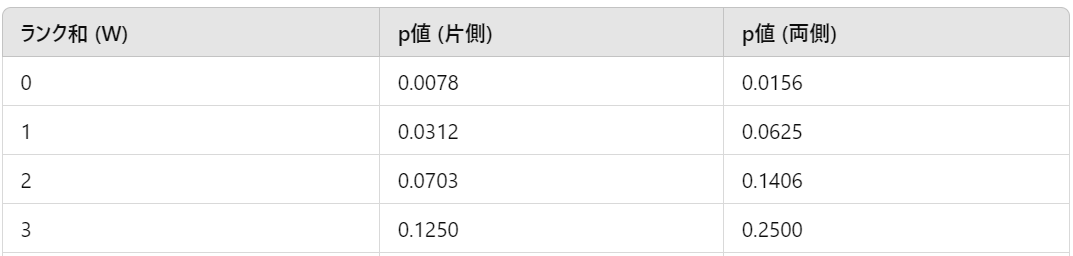
サンプルサイズが25以下なので、サインランク検定表から対応するp値を求めます。今回は”0.0156”です。
【5】有意差の判定
p値0.0156<有意水準0.05なので、従来のレシピと新しいレシピの味に有意な差があると結論づけられます。試食者の評価によると、新しいレシピの方が明らかに好まれていると結論付けることができます。



