この記事では”実験計画法とは”で解説した一因子実験と要因実験の”情報量の違い”について詳しく解説します。
この記事を読むことで実験データの構造を感覚的に理解することができるようになるはずです。
単一因子実験と要因実験
まず、単一因子実験と要因実験のそれぞれについて説明します。
単一因子実験とは
一度の実験で因子を1つずつ取り上げる実験方法を単一因子実験(一元配置実験)といいます。
たとえば、因子Aと因子Bの2つの最適な組み合わせを決定したい場合、①因子Bを固定して因子Aの最適水準を決定⇒②最適な因子Aで固定して因子Bを実験する。
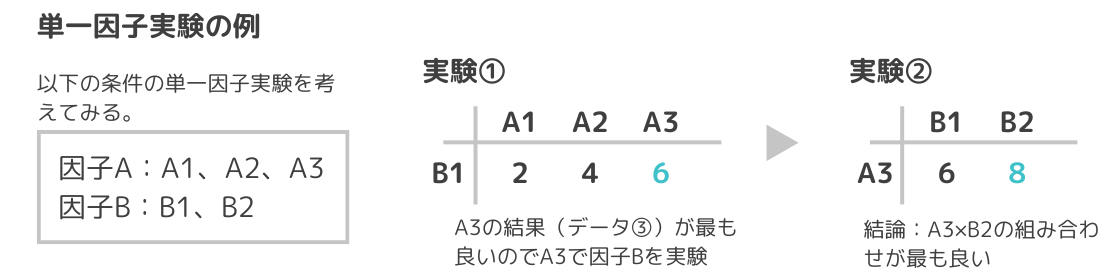
という具合に、因子を1つずつ取り上げて検証します。
単一因子実験の欠点としては、交互作用がある場合に誤った結論を導き出すことがあります。
要因実験とは
一方で、要因実験とは問題とする因子を同時に取り上げ、因子の水準全ての組み合わせを実験する方法です。
単一因子実験では交互作用がある場合、誤った結論を導き出すことがありますが、要因実験では交互作用がある場合でも正しく評価できます。
単一因子実験ではA3×B2の組み合わせが最も良いと結論付けたが、以下のように交互作用がある場合にはA2×B2の組み合わせが最も良いという結論になります。
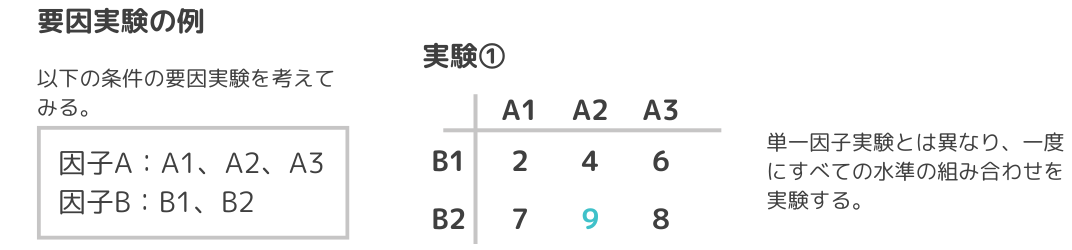
要因実験の欠点としては、総当たりで全ての水準を実験するため実験数が多くなる傾向にあります。この欠点を克服するために考えられたのが直交表などの実験方法です。
単一因子実験と要因実験の比較
それぞれの実験の特徴がわかったところで、単一因子実験と要因実験の違いをもう少し詳しく比較してみます。
要因実験の方が情報量が2倍多い
単一因子実験では”交互作用がある場合”に誤った結論を導き出すことがありますが、”交互作用がないとわかっている場合”には単一因子実験で十分なのでしょうか?
いいえ、十分ではありません。交互作用がないとわかっている場合でも、要因実験をしたほうが実験回数と得られる情報の精度という点で有利になります。
2因子、2水準の場合の単一因子実験と要因実験を表で比較してみます。
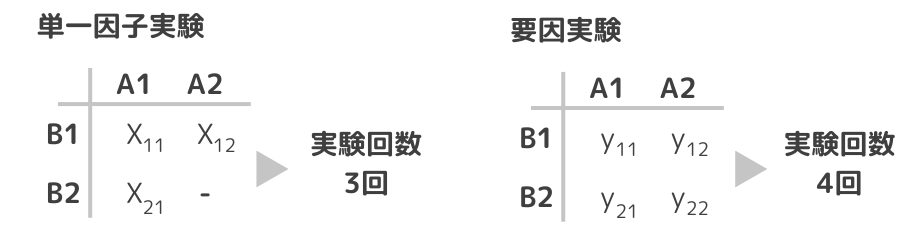
単一因子実験の場合は実験回数が3回、要因実験の場合は実験回数が4回になります。
次に実験から得られる情報量を比較してみます。

単一因子の場合、Aの主効果はX21-X11、Bの主効果はX12-X11で推定されます。
一方、要因実験の場合は、Aの主効果はy21-y11とy22-y12の2つで推定できることになります。Bの主効果の場合も同様にy12-y11とy22-y21の2つで推定できます。
つまり、要因実験は実験回数が1回しか多いだけにも関わらず、得られる情報量としては2倍あることになります。
仮に、単一因子実験で要因実験と同じ情報量を得ようとすると、実験数3回×2回=6回の実験が必要ということになります。
以上のことから、交互作用が存在しない場合でも要因実験をしたほうが実験回数と情報量の点から有利ということになります。
実験結果の情報量を図でわかりやすく解説
先ほどの説明をもっと感覚的に理解するには以下の図のようなイメージをするとよいと思います。
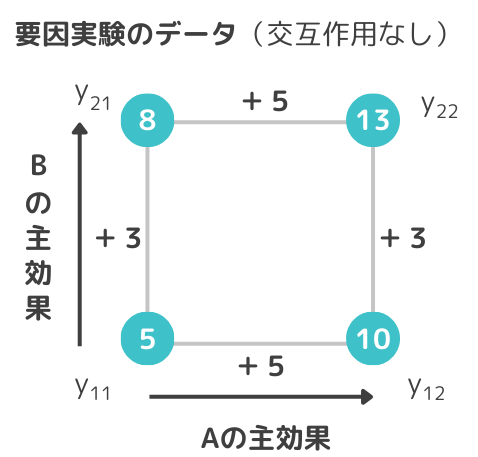
2因子、2水準の要因実験では、このようにAの主効果を横軸、Bの主効果を縦軸として考えてみます。すると、Aの主効果は”+5”、Bの主効果は”+3”となっていることがわかります。つまり、Aの主効果はy21-y11とy22-y12、Bの主効果はy12-y11とy22-y21の2つで推定できるということです。
次に単一因子実験を考えてみます。
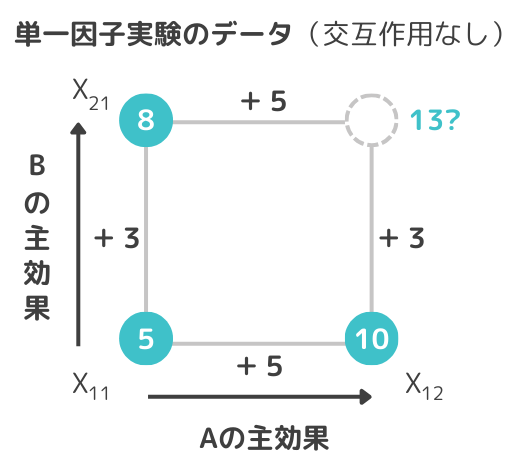
単一因子実験では、3つの実験データしかありません(上記の図では右上のデータが欠損しています)。そのため要因実験とは違い、Aの主効果はX21-X11、Bの主効果はX12-X11で推定ので精度が劣ることになります。交互作用のない場合は単一因子実験でもなんとなく右上のデータを予測することは可能です。
単一因子実験は使えない実験なのか?
これまでの説明から「じゃあ単一因子実験は使えない実験方法なのか?」という疑問が出てくるでしょう。
実際はそんなことはなく、例えば、技術的知見が十分にない開発初期の段階には単一因子実験で因子の性質を調べる実験は必要不可欠です。あるいは、因子と特性値について十分な技術的知見がある場合は、要因実験をしないでよいと考えられる水準の組み合わせを省いて、実験を効率的にできる場合もあります。
したがって、単一因子実験と要因実験は自身の経験や知識を考慮して、効率よく実験できる方を選択しましょう。