データ分析を進める中で統計検定の選択は非常に重要です。特に「パラメトリック検定」と「ノンパラメトリック検定」は、よく使われる2つの検定方法ですが、その違いや使い分けについて理解しているでしょうか?この記事では、ノンパラメトリック検定に焦点を当て、パラメトリック検定との違いや、ノンパラメトリック検定の種類について詳しく解説します。
パラメトリック検定とノンパラメトリック検定の違い
まず、パラメトリック検定とノンパラメトリック検定の基本的な違いを説明します。
パラメトリック検定とは
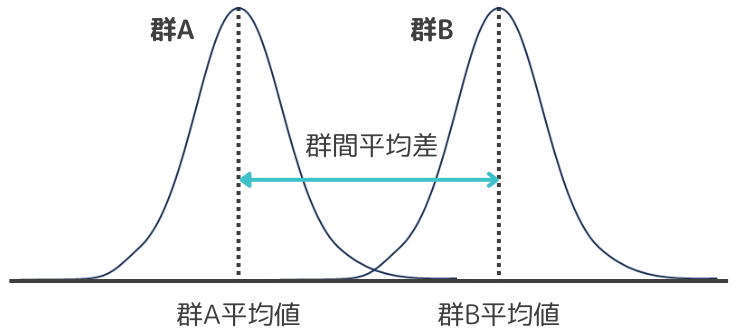
母集団の分布が正規分布に従うことを前提として行う検定法のことです。母集団が正規分布に従う場合、群間の平均値の差で有意差を判定します。代表的手法にt検定や分散分析があります。
ノンパラメトリック検定とは
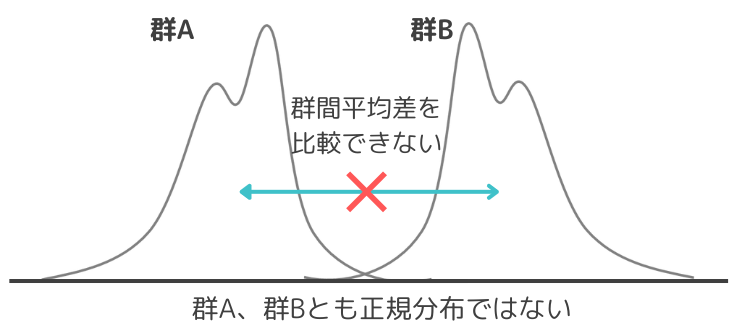
パラメトリック検定のように母集団の分布が正規分布に従うことを仮定しない検定法です。母集団の分布を用いない代わりに、データの大小の順序尺度を利用します。
ノンパラメトリック検定は、データが少なく、データが従う分布を仮定することが難しい場合に利用されます。つまり、どのようなデータにも適用することができるため非常に便利な検定方法です。
正規性を調べる方法
データが正規分布に従っているかどうかを確認する方法はいくつかあり、以下に代表的な方法を紹介します。
視覚的な方法
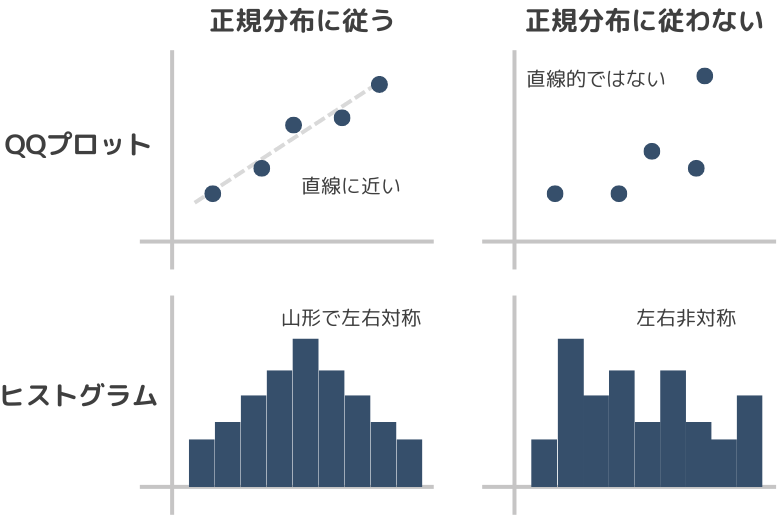
ヒストグラムやQQプロットを使用してデータの分布を視覚的に確認します。ヒストグラムはデータの頻度分布を示し、QQプロットはデータの分布が正規分布に従っているかどうかを視覚的に確認できます。QQプロットでデータ点が直線に近ければ、正規分布に従っていると判断できます。
統計的な方法
データが正規分布に従うかどうかを統計的に検定する方法として、シャピロ・ウィルク検定やコルモゴロフ・スミルノフ検定があります。シャピロ・ウィルク検定は、特に小規模なサンプルサイズに対して有効です。一方、コルモゴロフ・スミルノフ検定は、データの分布が任意の分布に従うかどうかを検定するために使用されます。
ノンパラメトリック検定を使う場面
- サンプルサイズが小さい
データの量が少ない場合(サンプルサイズ30未満)。
パラメトリック検定では信頼性が低くなることがある。 - データの分布が不明
データが正規分布に従うかどうかが不明な場合や明らかに正規分布から外れている場合。
例えば、非対称な分布や異常値が多く含まれるデータセットの場合、ノンパラメトリック検定が適しています。 - 順序データやカテゴリーデータ
データが数値ではなく、順位やカテゴリーである場合。
例えば、アンケート調査の結果や製品の評価など、順位が重要なデータに対して有効です。
”ノンパラメトリック検定の注意点”
本来、パラメトリック検定が適切なデータに対してノンパラメトリック検定を行うと、帰無仮説を棄却できるのにも関わらず帰無仮説を採用してしまう確率 (第2種の過誤、有意であるものを有意としない確率) が大きく上昇します。したがって、パラメトリック検定が適用可能な場合はパラメトリック検定を適用しましょう。
ノンパラメトリック検定の種類
ノンパラメトリック検定には様々な手法がありますが、ここでは基本的な4つの手法を紹介します。

データが”対応のあり、なし”、群数が”2群まはた3群以上の比較”によって使用する手法が異なります。
- 対応あり / 2群比較:ウイルコクソンの順位和検定(U検定)
- 対応あり / 3群以上の比較:クルスカルワリス検定
- 対応なし / 2群比較:ウイルコクソンの符号順位和検定
- 対応なし / 3群以上の比較:フリードマン検定


