母集団の分布が正規分布に従うことを仮定しない検定法であるノンパラメトリック検定にはいくつかの種類があります。この記事では、データが”3群以上の比較”かつ”対応のない”場合に使用する、クルスカルワリス検定について解説します。
クルスカルワリス検定とは
対応のない3群以上のデータ間の中央値に有意差があるかどうかを検定するノンパラメトリック手法です。データが正規分布していない場合、サンプルサイズが小さい場合に特に適しています。パラメトリックの一元配置分散分析(ANOVA)のノンパラメトリック版です。
”対応のある”3群以上のデータ間を検定する場合はフリードマン検定を使用します。
”対応あり”と”対応なし”とは?
対応あり:関連する2つのグループ(たとえば、同じ被験者の投薬前後の測定値を比較する場合)
対応なし:2つの独立したグループ(たとえば、異なるコーヒーの味を比較する場合)
クルスカルワリス検定の計算手順
以下クルスカルワリス検定の実施手順を解説します。
【1】仮説を立てる
- 帰無仮説(H0):3群以上の母集団の順位平均値は”同じ”
- 対立仮説(H1):3群以上の母集団の順位平均値は”異なる”
【2】両側検定、片側検定を決める
クルスカルワリス検定は”片側検定”のみです。
クルスカルワリス検定はなぜ”片側検定”のみ?
クルスカルワリス検定は複数のグループの中央値がすべて等しいかどうかの検定です。この検定では、帰無仮説が「すべてのグループの中央値が等しい」というもので、対立仮説が「少なくとも1つのグループの中央値が異なる」というものです。検定統計量が大きくなるほど、帰無仮説を棄却する傾向が強くなるため、カイ二乗分布を使ってp値を算出します。カイ二乗分布は右に裾を引いた形をしており、右側の尾部に検定統計量が位置するかどうかを基にp値を計算します。これが「片側検定」となる理由です。
【3】検定統計量を算出
- データのランク付け:全てのデータを昇順に並べ、それぞれに順位を付けする(同じ値には平均の順位を割り当てる)。
- ランクの合計:各グループのランクの合計を計算する。
- 検定統計量の計算:以下の式を用いて検定統計量Hを計算する。
ここで、$N$は全データ数、$k$はグループ数、$Ri$は各グループのランクの合計、$ni$は各グループのデータ数です。
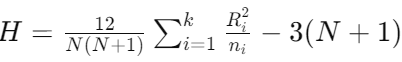
【4】p値を算出
カイ二乗分布を適用し、p値を算出する。
【5】有意差判定
- p値<有意水準0.05 ⇒ 帰無仮説を棄却し対立仮説を採択。3群以上の順位平均値に”有意差があるといえる”
- p値≧有意水準0.05 ⇒ 帰無仮説を棄却できず、3群以上の順位平均値に”有意差があるといえない”
【例題】クルスカルワリス検定をやってみよう!
では具体的な例題を使って、クルスカルワリス検定を実際に行ってみましょう。
例題:ペンギンの体重増加の比較
ある動物園が、3つの異なる餌のタイプ(餌A、餌B、餌C)を使用してペンギンの体重増加を比較する実験を行いました。各グループには6羽のペンギンが含まれており、一定期間後の体重増加(kg)を測定しました。このデータをもとに有意水準0.05でクルスカルワリス検定を行います。
| 餌A | 餌B | 餌C |
| 2.5 | 3.2 | 2.8 |
| 2.9 | 3.3 | 3.1 |
| 3.0 | 3.1 | 2.7 |
| 2.8 | 3.0 | 2.9 |
| 3.1 | 3.4 | 2.6 |
| 2.7 | 2.8 | 2.5 |
【1】仮説を立てる
・帰無仮説:餌A,餌B,餌Cの母集団の順位平均値は”同じ”
・対立仮説:餌A,餌B,餌Cの母集団の順位平均値は”異なる”
【2】検定方法
クルスカルワリス検定なので”片側検定”
【3】統計量を算出
- データのランク付け:全てのデータを昇順に並べ、それぞれに順位を付け。
- ランクの合計:各グループのランクの合計を計算する。
- 検定統計量の計算:以下の式を用いて検定統計量Hを計算する。

【4】p値を算出
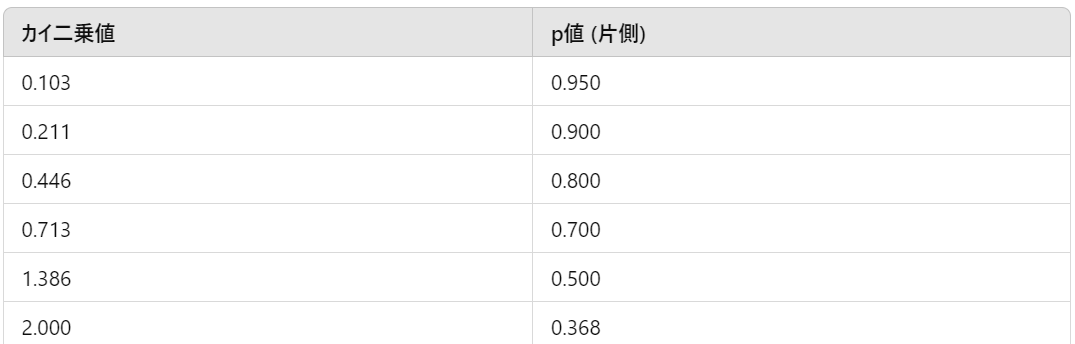
自由度は $k−1=2$ です。カイ二乗分布を用いてp値を求めます。
今回は統計量が”1.227”なので、p値は0.5~0.7の間となります。
【5】有意差の判定
p値≧有意水準0.05なので、帰無仮説を棄却できず餌A,餌B,餌Cの母集団の順位平均値は”同じ”と結論付けます。



