統計的仮説検定とは
統計的仮説検定は、母集団分布の母数に関する仮説の真偽を標本から検証するための統計的手法です。仮説検定は「帰無仮説」(H0)と「対立仮説」(H1)の2つの仮説を設定します。帰無仮説は、特定の条件や効果が存在しないことを示し、対立仮説はその条件や効果が存在することを示します。データを分析して、帰無仮説を棄却するかどうかを判断します。統計的仮説検定には多数の種類があり、t検定や分散分析などがあげられます。
例えば、新薬の効果を調べたい場合、「新薬は母集団において効果がある」という仮説を立てます。統計的仮説検定を用いて分析することでこの仮説が正しいかを判定することができます。
帰無仮説、対立仮説とは
データA、データBを比較するとき「AとBの母平均は異なる」と主張したい場合、それとは逆の「AとBの母平均は等しい」という仮説を立てます。このとき、主張したい仮説を対立仮説、逆の仮説を帰無仮説といいます。
【例】新薬の効果を検証する
帰無仮説(H0):新薬の効果が”ない”
対立仮説(H1):新薬の効果が”ある”
p値とは
p値は帰無仮説が正しいと仮定した場合に、観察されたデータまたはそれよりも極端なデータが得られる確率です。p値が小さいほど、帰無仮説が正しいという仮定に矛盾する証拠が強くなります。
たとえば、p値が0.01の時は帰無仮説が偶然生じる可能性が100回に1回(1%)です。つまり対立仮説である可能性が高くなります。
有意水準とは
有意水準(α)は、帰無仮説を棄却するための基準となる確率です。一般的には有意水準はα=0.05(5%)またはα=0.01(1%)が使用されます。
有意差判定
p値と有意水準を比較して、有意差があるかどうかを判断します。p値が事前に定めた「有意水準」より小さければ、帰無仮説は棄却され主張したいこと(対立仮説)が成立すると判断します。
例えば、p値が有意水準α=0.05よりも小さい場合は、主張したいことを誤る確率は5%より小さく、対立仮説が正しいと判断できます。反対にp値が有意水準α=0.05より大きい場合は、帰無仮説は棄却できず対立仮説が正しいとは判断できません。
- p値 ≤ 有意水準:帰無仮説を棄却し、有意差があると判断
- p値 > 有意水準:帰無仮説を棄却せず、有意差があるとはいえないと判断
対応のない、対応のある
2つのグループの比較で異なる集団について測定したデータは対応のないデータ、同じグループについて測定したデータは対応のあるデータという。
例えば、新薬の効果を検証する場合、同じ被験者での投薬前後を比較するため”対応のあるデータ”になります。男女の平均身長を比較する場合、男性と女性で異なるグループを比較するため、”対応のないデータ”になります。
- 対応なし:独立した2つのグループのデータを比較する検定。
- 対応あり:同じグループのデータを比較する検定。
両側検定、片側検定
データAとデータBを比較する場合、対立仮説には以下3つが考えられます。
1.母平均Aと母平均Bは”異なる”
母平均Aが母平均Bよりも大きいか小さいかはわからないが、いずれにせよ”異なる”という仮説です。この仮説での検定を両側検定といいます。
2.母平均Aは母平均Bよりも”大きい”
この仮説は片側検定(上側検定)といいます。
3.母平均Aは母平均Bよりも”小さい”
この仮説は片側検定(下側検定)といいます。
第1種の誤り、第2種の誤り、検出力
- 第1種の誤り(αエラー):帰無仮説が真であるのに、それを棄却する誤り。これは有意水準と同じ確率です。
- 第2種の誤り(βエラー):対立仮説が真であるのに、帰無仮説を棄却しない誤り。この誤りの確率はβで表されます。
- 検出力:検出力は1-βで表され、誤った帰無仮説を正しく棄却できる確率です。
”第1種の誤り”と”第2種の誤り”の関係
第1種の誤りと第2種の誤りはトレードオフの関係にあります。有意水準を低く設定すると、第1種の誤りが減少しますが、第2種の誤りが増加する可能性があります。そのため、バランスを考慮して有意水準を設定することが重要です。
統計的仮説検定の手順
- 手順1仮説を設定
- 帰無仮説(H0):研究対象の条件や効果がないことを示します。
- 対立仮説(H1):研究対象の条件や効果があることを示します。
- 手順2統計量を算出
データから統計量を算出します。統計量の計算方法は各検定の種類によって異なります。
- 手順3p値を算出
算出した統計量から分布表を使ってp値を求めます。分布には、正規分布、t分布、カイ二乗分布、F分布などがあり、検定の種類によって使う分布が異なります。
- 手順4有意水準の設定
有意水準(α)を決定します。有意水準は、帰無仮説を棄却するための基準となる確率で、一般的な有意水準は0.05(5%)です。
- 手順5有意差の判定
- p値 ≤ 有意水準:帰無仮説を棄却し、有意差があると判断
- p値 > 有意水準:帰無仮説を棄却せず、有意差があるとはいえないと判断
統計的仮説検定の種類
パラメトリック検定
パラメトリック検定は、データが特定の分布(通常は正規分布)に従うという前提の下で行われる検定です。以下は一般的なパラメトリック検定の例です。
- t検定:2つのグループの平均値を比較
- ANOVA(分散分析):3つ以上のグループの平均値を比較
- 多重比較法:3つ以上のグループの平均値を比較し、どの群間で有意差があるかを判定
ノンパラメトリック検定
ノンパラメトリック検定は、データが特定の分布に従う必要がない検定です。データの順位や符号を用いて検定を行います。以下は一般的なノンパラメトリック検定の例です。
- ウイルコクソンの順位和検定(U検定):2つの関連したグループの中央値の比較
- クルスカルワリス検定:3つ以上の関連したグループの中央値の比較
- ウイルコクソンの符号順位和検定:2つの独立したグループの中央値の比較
- フリードマン検定:3つ以上の独立したグループの中央値の比較
統計的仮説検定の応用”実験計画法”
統計的仮説検定を応用した手法に実験計画法があります。実験計画法とは、「多数の実験条件の組み合わせを総当たりまたは一部の組み合わせで実験を行い、最適な条件を効率よく見つける手法」です。たとえば、4因子の実験する場合、すべての組み合わせを検証しようとすると24=16回の実験をする必要がありますが、実験計画法の直交表を使うとその半分の8回で検証できます。
【具体例】t検定の計算手順
例題:グループ間のテスト点数比較
以下2つのグループの学生のテスト得点を比較します
・グループA:85, 88, 90, 92, 85
・グループB:80, 82, 85, 87, 83
【1】仮説を立てる
・帰無仮説:グループAとグループBの平均得点に差はない。
・対立仮説:グループAとグループBの平均得点に差がある。
【2】検定方法
グループAとグループBの平均得点は”異なる”なので”両側検定”
【3】統計量を算出する
・各グループの平均値を計算
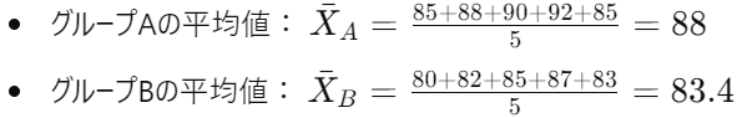
・各グループの標準偏差を計算
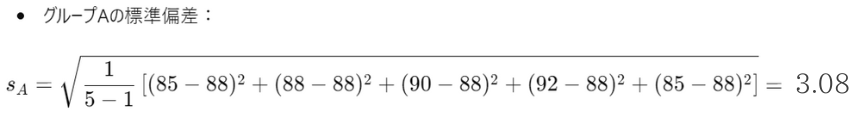
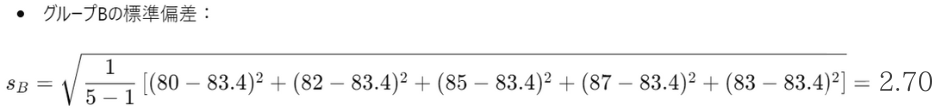
・t値を計算
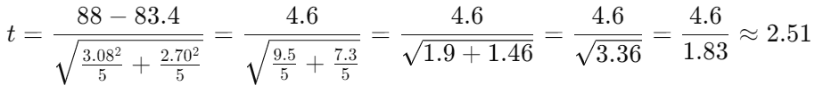
【4】p値を算出、有意差判定
t分布表を使って、t値2.51に対応するp値を求めます。p値が”0.0363”でした。
【5】有意差の判定
p値≤有意水準0.05のため、帰無仮説を棄却し、有意差があると判断します。

