実験計画法｜3水準直交表を例題で解説（交互作用なしの場合）

実験計画法とは、「多数の実験条件の組み合わせを総当たりまたは一部の組み合わせで実験を行い、最適な条件を効率よく見つける手法」です。

水準の組み合わせを総当たりで行う実験を要因配置実験（二元配置分散分析など）、一部の水準の組み合わせを行う実験を部分配置実験（直交表など）といいます。

この記事では部分配置実験に分類される”3水準の直交表（交互作用なしの場合）”について解説します。

実験計画法の3水準直交表とは

総当たりで行う要因実験では、因子の数が多くなるにつれ水準組み合わせが増えるため、実験回数が多くなります。一方、部分配置実験では実験回数を減らしつつ、多数回の実験を均一な場で実施することが可能となり、効率よく実験することができます。

3水準の直交表は、直交表の本体に出てくる数字（水準数）が”1、2、3”の3種類であるため、”3水準”と呼ばれます。水準数が”1、2”の2種類の場合は”2水準の直交表”となります。

3水準直交表｜L9(34)の名称の意味

3水準直交表にはL₉(3⁴)、L₂₇(3¹³)のように種類が複数あります。これらの名称には以下の意味があります。

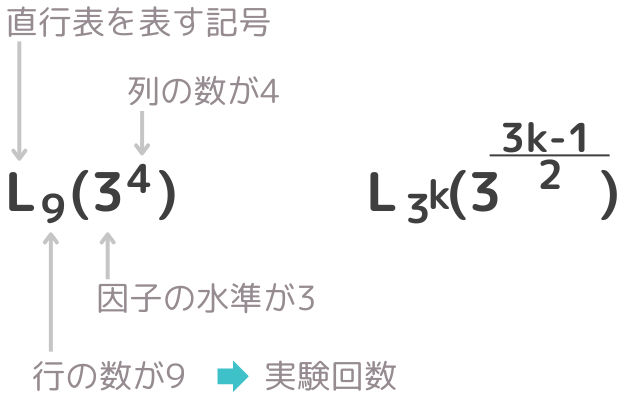
L₉(3⁴)の場合、”9”が行の数（実験回数）、”3”は3水準系の実験であること、”4”は列の数を表しています。式で書くと右図になります。ちなみに、”L”は直交表を表す記号で、直交表がラテン方格（Laten square）を発展させたことが由来しています。

3水準直交表｜L9(34)の見方

以下はL₉(3⁴)の直交表です。

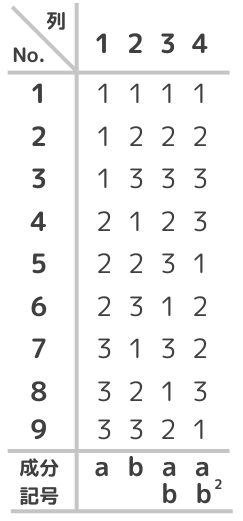
No.1～9は実験番号を表しています。L₉(3⁴)では9回の実験を行うことになります。表中の”１”と”２”と”３”は各因子の水準を表しています。因子は任意の列に割り付けすることができ、割り付け方はのちほど説明します。成分記号は割り付け時に使用したり、交互作用が出る列を確認するのに使います。

L₉(3⁴)を見ると2つの列のどの組み合わせにおいても、（１，１）、（１，２）、（１，3）、（２，１）、（２，２）、（２，3）、（3，１）、（3，２）、（3，3）の9通りあり、必ず同じ回数ずつ現れるようになっています。これが直交表の性質です。

3水準直交表｜L9(34)の因子割り付け方法（交互作用なしの場合）

L₉(3⁴)の直交表を実際にどのように使用するか解説します。
各3水準の3つの因子（A,B,C）、交互作用なしの場合を考えてみましょう。

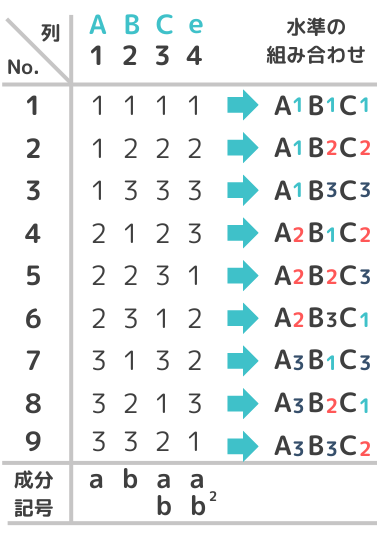
L₉(3⁴)直交表にA,B,Cの各因子を任意の列に割り付けます。今回は1列目にA、2列目にB、3列目にCを割り付けます。残った4列目が誤差項（e）となります。表中の”１”と”２”と”３”は各因子の水準であり、実験番号の内容は以下になります。

• No.1：A1B1C1
  　　　⇒（Aの水準1、Bの水準1、Cの水準1）
• No.2：A1B2C2
  　　　⇒（Aの水準1、Bの水準2、Cの水準2）
• 以降も同じ

L₉(3⁴)の直交表では9回の実験で各因子の水準間の比較をすることができます。もし、3因子すべてを実験しようと思ったら3³＝27回の実験をする必要がありますが、直交表では9回で検証できるんです！

少ない実験回数で検証できる理由

直交表で実験回数が減らせる理由についてL₉(3⁴)のデータの構造モデルから説明します。

1. 実験No.1～9をx₁~x₉と置きます。交互作用はないので①のように書けます。
2. 因子Aを例にとると②の式では因子B,Cが3つの式に均等に入っています。
3. ③のように式を整理すると”α₁-α₂-α₃+誤差”が得られます。
   したがって、A₁でのデータの平均値、A₂でのデータの平均値、A₃でのデータの平均値を比較すればA₁とA₂のとA₃比較になっていることがわかります。他の因子についても同様です。

3水準直交表の種類

L₉(3⁴)の他にL₂₇(3¹³)、L₈₁(3⁴⁰)などがあります。
L₂₇(3¹³)は実験回数27回、L₈₁(3⁴⁰)は実験回数81回です。実験回数の多い直交表を使うと割り付け方法によって9水準の因子を割り付けることも可能です。

【例】3水準直交表（交互作用なし）のL9(34)の実施手順

では、実際にL₉(3⁴)を使った実験を具体例で解説していきます。
エクセルを使った計算方法は”エクセルで3水準直交表の作り方”で解説してます。

例題：自動掃除ロボットの開発。L₉(3⁴)を使った実験
ドクター・フラフは、最強の自動掃除ロボット「クリーンマスター」を開発するために、実験を行うことにしました。彼は、掃除ロボットの性能を最大化するために、いくつかの要因を調査することに決めました。そこで、3つの因子（ブラシの種類、掃除速度、バッテリータイプ）を選び、それぞれ3つのレベルで実験を行うことにしました。ドクター・フラフはL₉(3⁴)直行表を使用して、効率的に実験を進めます。交互作用はないものとします。

【1】直交表の割り付け
　A,B,Cは交互作用はないものとして以下のように割り付けを行った。

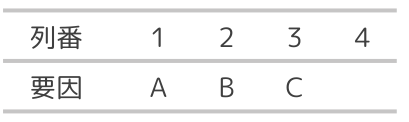
【2】実験結果
　実験結果を以下に示す。

	No.1	No.2	No.3	No.4	No.5	No.6	No.7	No.8	No.9
掃除効果	65	85	75	65	80	60	90	75	85

【3】各要因の平方和、平均平方和、F₀を計算
　計算式は以下の通り。

【4】分散分析表を作成

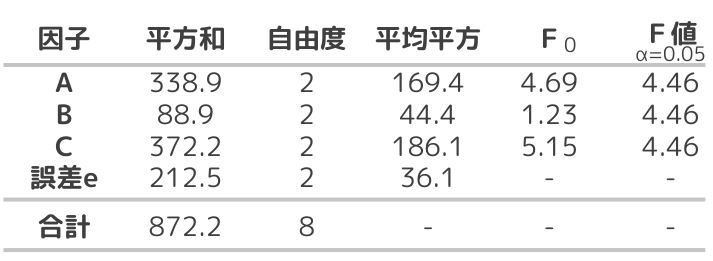
【結論】
この分散分析結果から、F値＜F₀である因子A（ブラシの種類）、因子C（バッテリータイプ）が影響力のある因子であることがわかります。因子B（掃除速度）はF値＞F0であることから影響が少ないことが示されています。

これにより、最強の自動掃除ロボットを作るためには、ブラシの種類、バッテリータイプが重要であると結論づけられます。