実験計画法とは、「多数の実験条件の組み合わせを総当たりまたは一部の組み合わせで実験を行い、最適な条件を効率よく見つける手法」です。
水準の組み合わせを総当たりで行う実験を要因配置実験(二元配置分散分析など)、一部の水準の組み合わせを行う実験を部分配置実験(直交表など)といいます。
この記事では部分配置実験に分類される”2水準の直交表”について解説します。
実験計画法の2水準直交表とは
総当たりで行う要因実験では、因子の数が多くなるにつれ水準組み合わせが増えるため、実験回数が多くなります。一方、部分配置実験では実験回数を減らしつつ、多数回の実験を均一な場で実施することが可能となり、効率よく実験することができます。
2水準の直交表は、直交表の本体に出てくる数字(水準数)が”1”と”2”の2種類であるため、”2水準”と呼ばれます。
3水準の場合は”3水準直交表を例題で解説(交互作用なしの場合)”で解説しています。
2水準直交表|L8(27)の名称の意味
2水準直交表にはL4(23)、L8(27)のように種類が複数あります。これらの名称には以下の意味があります。
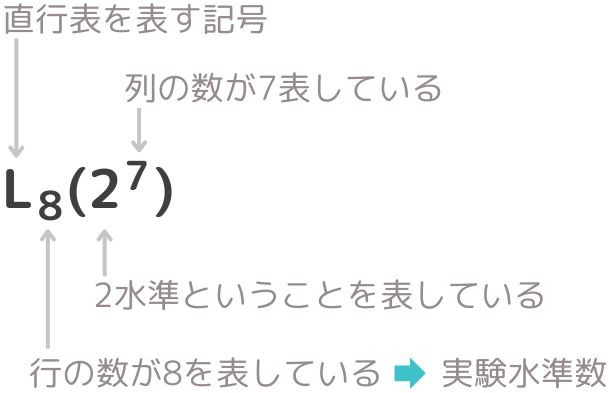
L8(27)の場合、”8”が行の数(実験回数)、”2”は2水準系の実験であること、”7”は列の数を表している。ちなみに、”L”は直交表を表す記号で、直交表がラテン方格(Laten square)を発展させたことが由来している。
2水準直交表|L8(27)の見方
以下はL8(27)の直交表です。

No.1~8は実験番号を表しています。L8(27)では8回の実験を行うことになります。表中の”1”と”2”は各因子の水準を表しています。因子は任意の列に割り付けすることができ、割り付け方はのちほど説明します。成分記号は割り付け時に使用したり、交互作用が出る列を確認するのに使います。
L8(27)を見ると2つの列のどの組み合わせにおいても、(1,1)、(1,2)、(2,1)(2,2)の4通りあり、必ず同じ回数ずつ現れるようになっています。これが直交表の性質です。
2水準直交表|L8(27)の因子割り付け方法(交互作用なしの場合)
L8(27)の直交表を実際にどのように使用するか解説します。
各2水準の4つの因子(A,B,C,D)、交互作用なしの場合を考えてみましょう。”交互作用がある場合”は割り付け方が異なるので注意してください。
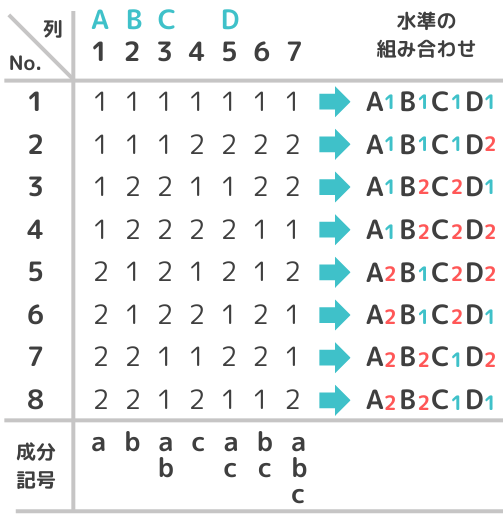
L8(27)直交表にA,B,C,Dの各因子を任意の列に割り付けます。今回は1列目にA、2列目にB、3列目にC、5列目にDを割り付けます。表中の”1”と”2”は因子の水準であり、No.1はA1B1C1D1(Aの水準1、Bの水準1、Cの水準1、Dの水準1)、No.2はA1B1C1D2(Aの水準1、Bの水準1、Cの水準1、Dの水準2)となります。
L8(27)の直交表では8回の実験で各因子の水準間の比較をすることができます。もし、4因子すべてを実験しようと思ったら24=16回の実験をする必要がありますが、直交表ではその半分の工数で検証できます。すごく効率的ですね!
少ない実験回数で検証できる理由
直交表で実験回数が減らせる理由についてL8(27)のデータ構造模型から説明します。

- 実験No.1~8をx1~x8と置きます。交互作用はないので①のように書けます。
- 因子Aを例にとると②の式では因子B,C,Dが両方の式に均等に入っています。
- ③のように式を整理すると”α1-α2+誤差”が得られます。
したがって、A1でのデータの平均値とA2でのデータの平均値を比較すればA1とA2の比較になっていることがわかります。他の因子についても同様です。
このように因子Aの各水準でのデータの平均値をとれば因子Bの影響が均等に入っており、因子Bの各水準でのデータの平均値をとれば因子Aの影響が均等に入っているとき、”因子Aの主効果と因子Bの主効果は直交している”といいます。だから、直交表というのですね!
2水準直交表の種類
L8(27)を中心に説明してきましたが、他にもL4(23)、L16(215)、L32(231)などがあります。
L4(23)は実験回数4回、L16(215)は実験回数16回、L32(231)は実験回数32回です。
因子の割り付け方やデータの構造はL8(27)と同様です。
【例】交互作用なしのL8(27)の実施手順
では、実際にL8(27)を使った実験を具体例で解説していきます。
例題:最強のコーヒーを作るL8(27)を使った実験
朝の目覚めを完璧にするために、コーヒー愛好家のジョンは「最強のコーヒー」を作り出すことに決めました。彼はさまざまな要因がコーヒーの味に与える影響を評価するために、実験計画法を用いることにしました。そこで、ジョンは4つの因子(コーヒー豆の種類、焙煎時間、抽出方法、水の温度)を選び、それぞれ2つのレベルで実験を行うことにしました。ジョンは、限られたリソースで効率的に実験を行うために、L8(27)直交表を使用しました。ここでは4つの因子に交互作用はないものとします。
因子の設定
- 因子A:コーヒー豆の種類(A1:アラビカ、A2:ロブスタ)
- 因子B:焙煎時間(B1:短い、B2:長い)
- 因子C:抽出方法(C1:ドリップ、C2:エスプレッソ)
- 因子D:水の温度(D1:低温、D2:高温)
実験結果
| No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | |
| 味の強度 | 60 | 70 | 75 | 85 | 65 | 80 | 90 | 95 |
【1】直交表の割り付け
A,B,C,Dは交互作用はないものとして以下のように割り付けを行った。

【2】各要因の平方和を計算
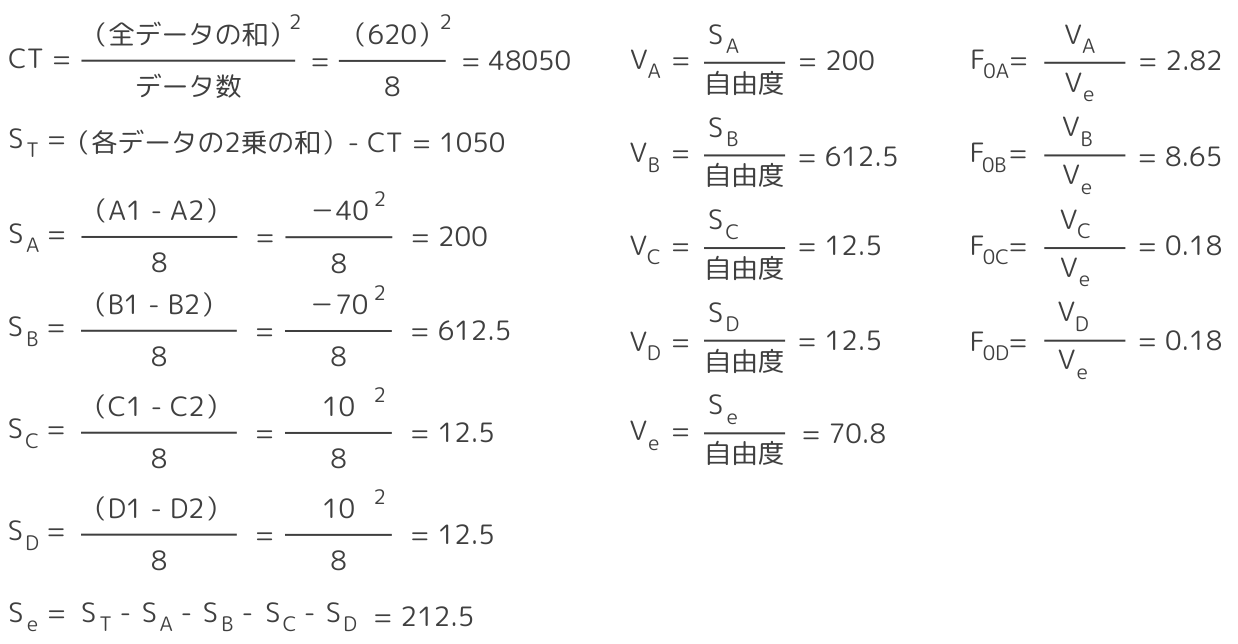
【3】分散分析表を作成
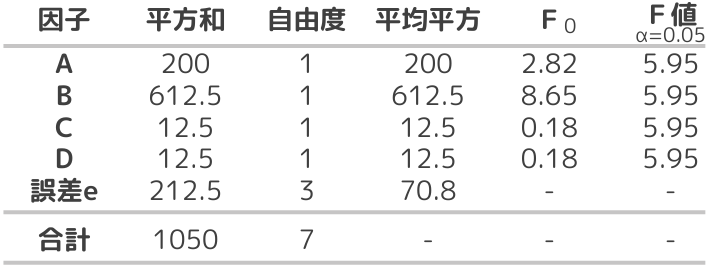
【結論】
この分散分析結果から、F値<F0である因子B(焙煎時間)が最も影響力のある因子であることがわかります。因子A(コーヒー豆の種類)、因子C(抽出方法)、因子D(水の温度)はF値>F0であることから影響が少ないことが示されています。
これにより、最強のコーヒーを作るためには、長い焙煎時間の豆を使うことが最適であると結論づけられます。