3群以上の平均値の有意差を調べる場合、分散分析(ANOVA:analysis of variance)を使用しますが、分散分析は全体的な平均値の相違を調べる方法であり、どの群間に有意差があるかは把握できません。そのため、分散分析で相違が認められた場合は、どこの群間に有意差があるか多重比較法によって検証する必要があります。
この記事では”なぜ多重比較が必要なのか”と”多重比較法の種類と選び方”について多重比較法を初めて聞く人にもわかりやすく解説します。
多重比較法とは?
多重比較法とは、3群以上の母平均を比較する場合において”どの群間で有意差があるか”を検討する分析手法です。冒頭説明した通り、分散分析は全群に対して検定を行うため、全体的な平均値との相違を調べることはできますが、どの群間に有意差があるかは把握できません。そのため、分散分析で有意差が認められた場合は多重比較法を使ってどこの群間に有意差があるかを調べる必要があります。多重比較では複数の比較(検定)を同時に行います。
多重比較法と分散分析の関係
分散分析は3群以上における”全体の平均値との相違を比較”、多重比較法は3群以上における”群間との相違を比較”します。
先ほど、「分散分析で有意差があった場合は、多重比較法を使ってどこの群間に有意差があるか調べる必要がある」としましたが、必ずしも”分散分析⇒多重比較法”と順を追って分析する必要はありません。どの群間に有意差があるかを調べたいのなら、最初から多重比較法を使って分析しても大丈夫です。
”分散分析⇒t検定”ではダメな理由
例えば、要因Aが3水準(A1、A2、A3とする)で分散分析を行い、有意差があるという結果が出た。どの水準が有意であったか検証するため、それぞれの組み合わせでt検定を行ってみる。
組み合わせは”A1×A2”、”A1×A3”、”A2×A3”の3通りです。有意水準は一般的な5%とします。有意水準は言い換えれば正しく有意であると判断できる確率が95%あるということです。つまり、3通りとも正しく判断できる確率が95%×95%×95%=85.7%であり、14.3%は1回は間違えて判定していることになります。
多重比較による誤検出のリスク
上記の通り、有意水準を0.05と設定して1回の検定を行う場合、誤って有意と判断される確率は5%ですが、検定を繰り返すこと(多重比較)で誤検出のリスクが上昇します。この”誤検出のリスク”を統計学的ルールにしたがって抑える検定方法が”多重比較法”です。
多重比較法の”誤検出のリスク”を押さえる調整方法
”誤検出のリスク”を統計学的ルールにしたがって抑える手法としては以下2つがあります。
① 有意水準の調整
例えば3群の比較を行う場合、この有意水準を5%よりも小さい1.67%に調整するします。これにより、全体の誤検出のリスクを5%に抑えることができます(3回とも正解する確率:98.339%×98.339%×98.339%=95%)。この方法の一例としてボンフェローニ補正があり、k個の比較に対して有意水準をα/kに調整します。
② 分布自体の調整
検定統計量が従う分布にはt分布やF分布などがありますが、多重比較には独自のスチューデント化されたq分布など他の分布を適用します。例えば、ダネットの多重比較法では、各ペアごとの比較を行う際に、q分布を利用して有意性を判断します。これにより、複数の比較における誤検出のリスクを適切に管理することができます。
多重比較法の種類と特徴
多重比較法には以下の7種類があります。詳細は別の記事で解説するとして、ここでは各手法の概要をお伝えします。
1.ボンフェローニ法
【特徴】
比較する群の数が少ない場合に適用。非常に保守的であるため、誤検出率を低く保つ。
【計算方法】
k個の比較を行う場合、有意水準αをkで割り、各検定に対してα/kを適用。p値がα/k以下であれば、その比較は有意とされる。
【具体例】
5つの比較を行う場合、有意水準が0.05ならば、各比較の有意水準は0.05/5 = 0.01となる。
2.ホルム法
【特徴】
逐次的な比較が必要な場合に適用。ボンフェローニ法よりもパワーが高く、多くの真の差異を検出できる。
【計算方法】
すべてのp値を昇順に並べ、最小のp値に対してα/kを適用し、有意でなければ次のp値に対してα/(k-1)を適用する。この手順を繰り返し、p値が有意水準を下回るかどうかを評価する。
【具体例】
p値が0.01, 0.03, 0.04の場合、最初の0.01に対して0.05/3を適用、次に0.03に対して0.05/2を適用する。この方法では、最小のp値0.01は0.0167(0.05/3)より小さいため有意とされ、次のp値も同様に評価される。
3.チューキー法
【特徴】
平均のペア比較が必要で、かつ標本サイズが同じ場合に適用。全体の誤検出率を管理し、信頼性が高い。
【計算方法】
q分布を用いて、各ペアごとの平均差を比較する。各群の平均の差をq統計量で評価し、その差が有意かどうかを判断。
【具体例】
3群の平均を比較する場合、各群の平均差をq分布に基づいて評価。例えば、A群とB群の平均差が有意であるかどうかをq分布の臨界値と比較する。
4.シェッフェ法
【特徴】
任意の線形対比を評価する場合に適用。非常に柔軟で、保守的な手法。
【計算方法】
F分布を使用し、すべての可能な線形対比を評価。任意の対比に対して、シェッフェの臨界値を計算し、有意性を判断する。
【具体例】
すべての群の平均を組み合わせて、特定の対比を評価する場合に使用。例えば、A群とB群の平均と、C群とD群の平均の差を評価する。
5.ダネット法
【特徴】
一つの基準群と他の群を比較する場合に適用。基準群との比較に特化している。
【計算方法】
基準群と他の群の平均差を比較し、特定の分布(q分布)を使用して評価する。
【具体例】
新薬と対照群の比較に使用し、各群の平均を基準群と比較。例えば、新薬群A、B、Cと対照群を比較し、各群の平均差をq分布に基づいて評価する。
6.チューキー・クレーマー法
【特徴】
平均のペア比較が必要で、標本サイズが異なる場合に適用。標本サイズの違いを考慮した方法。
【計算方法】
チューキー法と同様にq分布を使用するが、各群の標本サイズの違いを考慮した計算を行う。
【具体例】
3群の標本サイズがそれぞれ異なる場合に、各群の平均差を評価。各比較において標本サイズを考慮したq統計量を計算し、有意性を判断する。
7.ウイリアムズ法
【特徴】
線形の増加や減少を検出する場合に適用。順序付きデータに対して有効。
【計算方法】
順序付きデータの傾向を評価するために、特定の統計量を使用。増加または減少の一貫した傾向を検出する。
【具体例】
薬剤の投与量が増加するにつれて効果が増加するかどうかを評価。例えば、異なる投与量の薬剤群間で効果の線形増加を検証する。
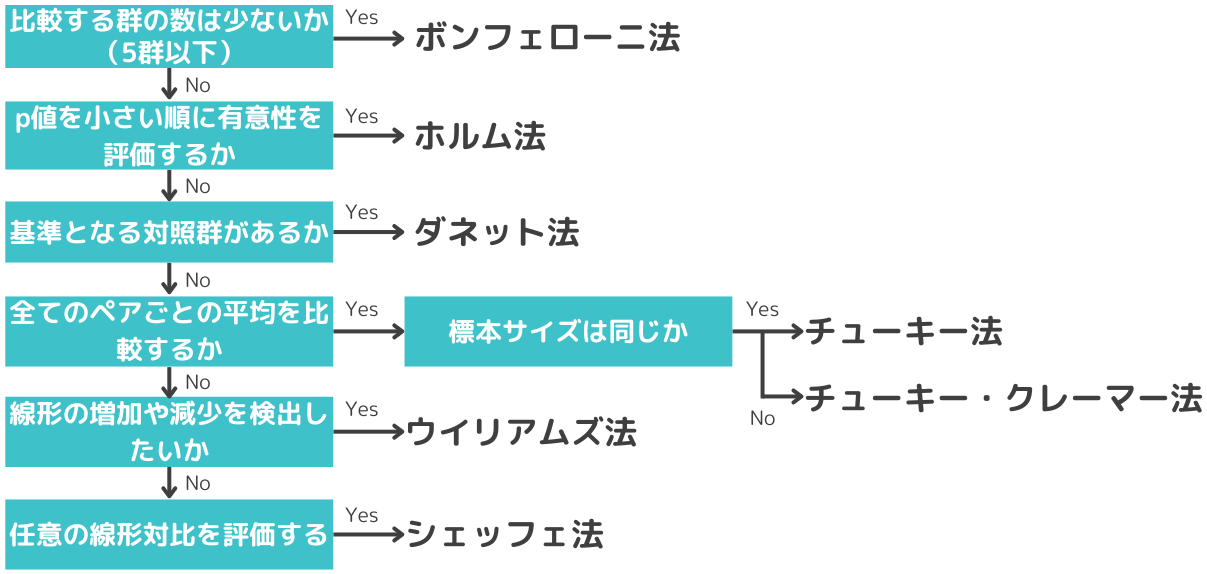
多重比較法の選択基準
多重比較法は種類が多く、どの手法を使って分析したらよいか迷ってしまうかもしれません。
ここでは各手法の特徴を一覧にまとめわかりやすく、さらにどの手法を使えばよいかフローチャートにまとめました。
多重比較法の特徴一覧
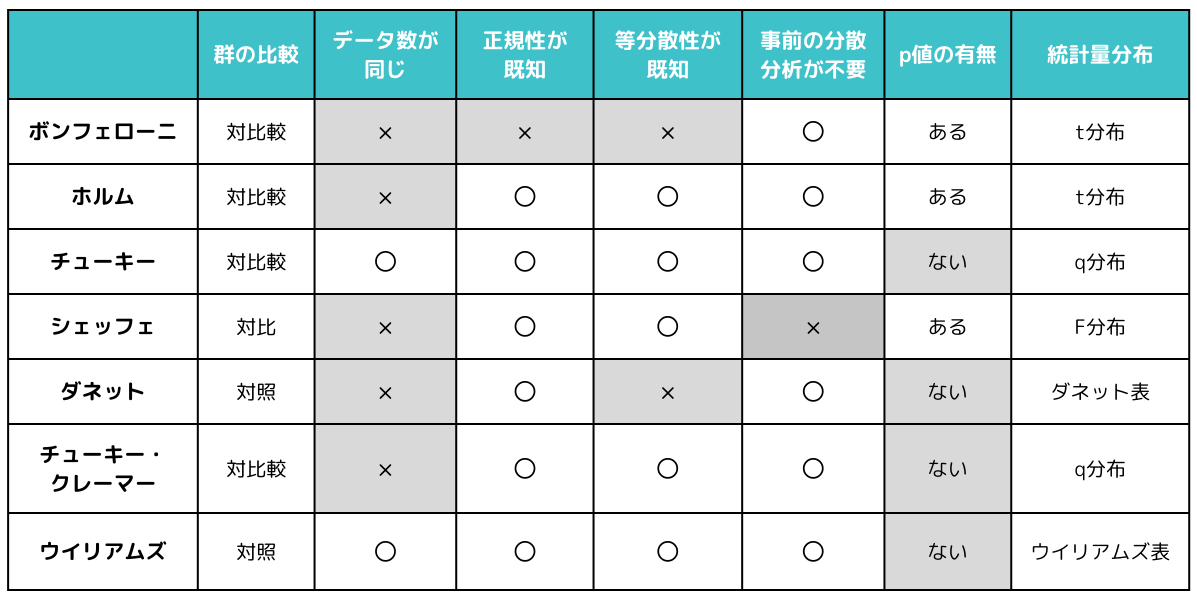
対比較:比較する群すべての組み合わせについて検討する方法
対照:対象とする群と他の群との組み合わせについて検討する方法
対比:方法は2つ。群をグループ化して比較する方法、群別平均の大小関係の傾向を把握する方法
※詳細は各多重比較法の紹介記事で解説。
多重比較法の選択フローチャート