実験計画法｜3水準直交表を例題で解説（交互作用ありの場合）

実験計画法とは、「多数の実験条件の組み合わせを総当たりまたは一部の組み合わせで実験を行い、最適な条件を効率よく見つける手法」です。

水準の組み合わせを総当たりで行う実験を要因配置実験（二元配置分散分析など）、一部の水準の組み合わせを行う実験を部分配置実験（直交表など）といいます。

この記事では部分配置実験に分類される”3水準の直交表（交互作用ありの場合）”について解説します。

実験計画法の3水準直交表とは

要因実験では、総当たりで実験を行うため因子の数が多くなるにつれ水準組み合わせが増え、実験回数が多くなります。一方、直交表を使った部分配置実験では実験回数を減らしつつ、多数回の実験を均一な場で実施することが可能となり、効率よく実験することができます。

直交表の表中に出てくる数字（水準数）が”1、2、3”の3種類であるため、”3水準”と呼ばれます。水準数が”1、2”の2種類の場合は”2水準の直交表”となります。また、交互作用がある場合は”交互作用なしの場合”とは異なり、因子の割り付け方に注意が必要です。

3水準直交表｜L27(313)の名称の意味

3水準直交表にはL₉(3⁴)、L₂₇(3¹³)のように種類が複数あります。これらの名称には以下の意味があります。

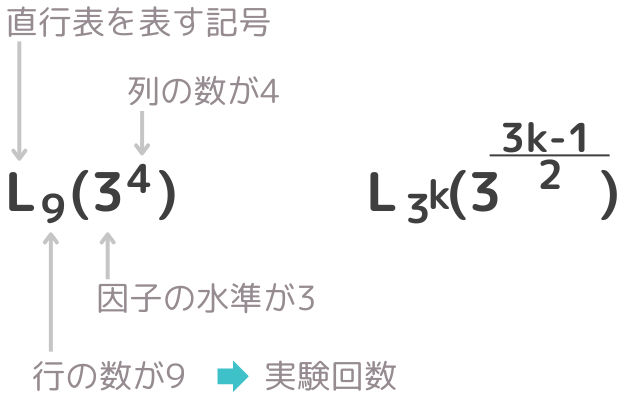
L₉(3⁴)の場合、”9”が行の数（実験回数）、”3”は3水準系の実験であること、”4”は列の数を表しています。式で書くと右図になります。ちなみに、”L”は直交表を表す記号で、直交表がラテン方格（Laten square）を発展させたことが由来しています。

3水準直交表｜L27(313)の見方

以下はL₂₇(3¹³)の直交表です。

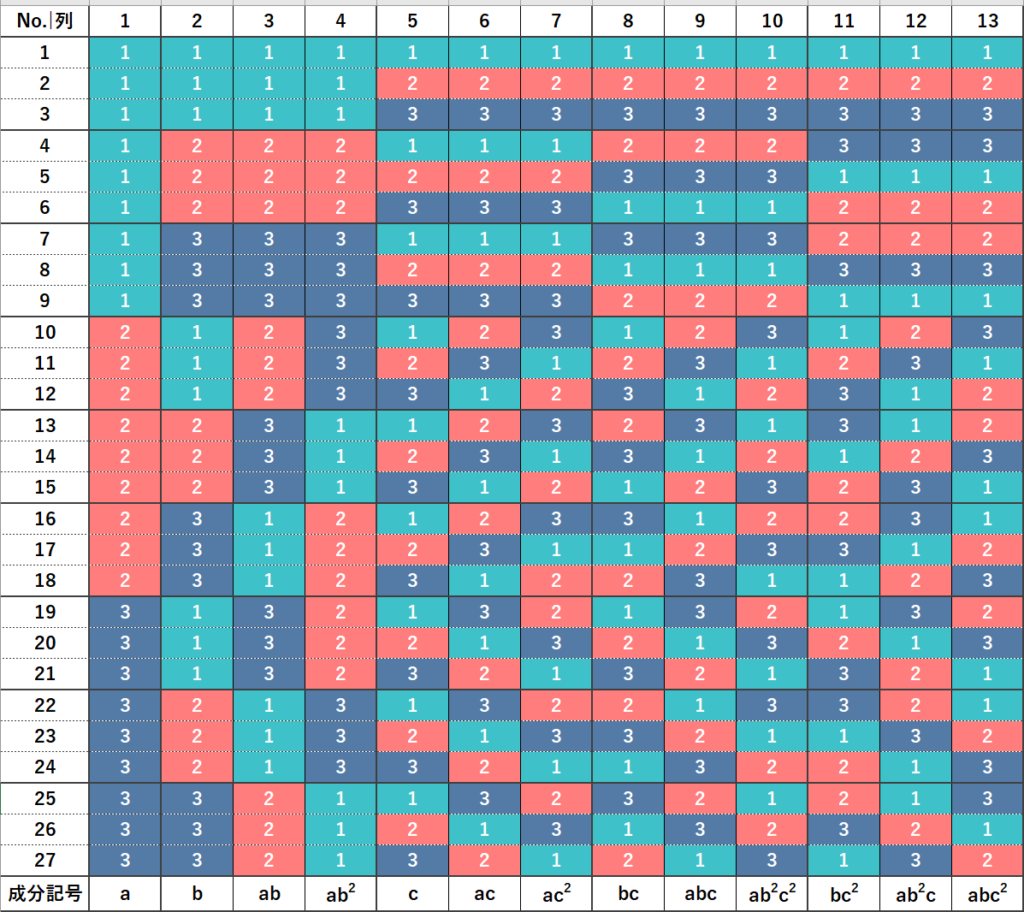
No.1～27は実験番号を表しています。L₂₇(3¹³)では27回の実験を行うことになります。表中の”１”と”２”と”３”は各因子の水準を表しています。因子は任意の1～13列に割り付けすることができ、割り付け方はのちほど説明します。

L₂₇(3¹³)を見ると2つの列のどの組み合わせにおいても、（１，１）、（１，２）、（１，3）、（２，１）、（２，２）、（２，3）、（3，１）、（3，２）、（3，3）の9通りあり、必ず同じ回数ずつ現れるようになっています。これが直交表の性質です。

また、2つの因子の交互作用は2水準の場合には1つの列に出ましたが、3水準の場合は2つの列に出てきます。
3水準の場合、各列の自由度は”２”であり、2つの因子の交互作用の自由度は”４”となるためです。

3水準直交表｜L27(313)の因子割り付け方法（交互作用なしの場合）

交互作用が”ない場合”と”ある場合”では直交表への割り付け方が異なります。交互作用がある場合は、どの列に交互作用が出るかを考えて割り付けを行う必要があります。ここでは交互作用がある場合の割り付け方をL₂₇(3¹³)を使って解説します。

割り付け方法１｜交互作用表を使う

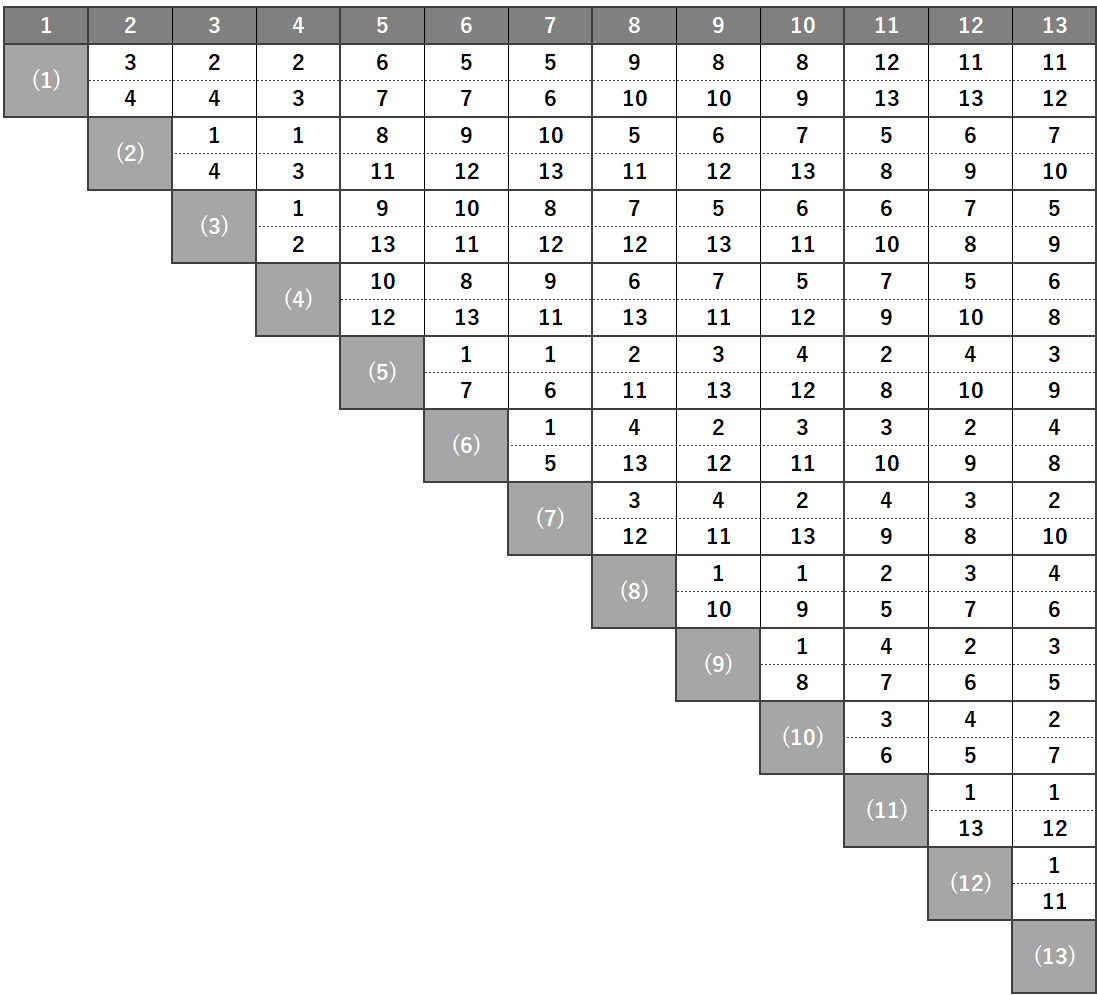
１つ目は直交表に付属している交互作用表を使う方法です。この表の見方は、例えば”4列目”と”6列目”との交互作用を求めるときは、”4行目の6列目”の数字を確認します。この場合は”8”と”13”になるので、4列目と6列目の交互作用は8列目と13列目に出ることがわかります。

割り付け方法2｜線点図を使う

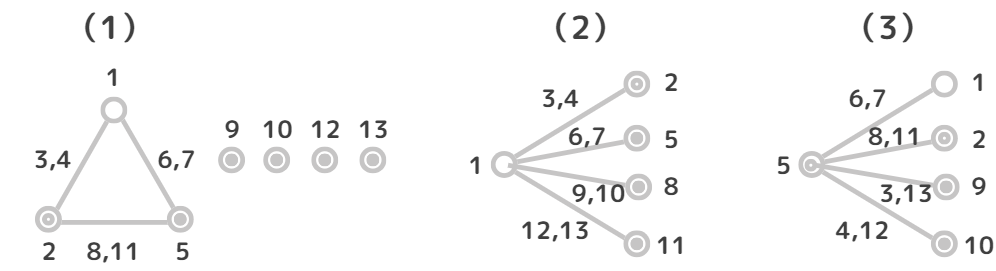
２つ目は線点図を使う方法です。線点図の数字は列番号を表します。2つの点を結ぶ線は交互作用を表しています。
たとえば、左図（1）は”点1”と”点2”を結ぶ線に”3,4”とあるので、1列目と2列目の交互作用は3列目と4列目に出ることがわかります。線点図はどの列に交互作用が出るかぱっと見でわかるのでおすすめです。

3水準直交表の種類

L₂₇(3¹³)の他にL₉(3⁴)、L₈₁(3⁴⁰)などがあります。
L₉(3⁴)は実験回数9回、L₈₁(3⁴⁰)は実験回数81回です。L₂₇(3¹³)のように実験回数の多い直交表を使うと割り付け方法によって9水準の因子を割り付けることも可能です。

L₉(3⁴)を使った実験手順は”3水準の直交表（交互作用なしの場合）”で解説しています。

【例】3水準直交表（交互作用なし）のL27(313)の実施手順

では、実際にL₂₇(3¹³)を使った実験を具体例で解説していきます。

例題：万人受けするおいしいチョコレートを目指して。L₂₇(3¹³)を使った実験
チョコレート職人のボブは万人受けするおいしいチョコレートを作るために、実験を行うことにしました。ボブは、チョコレートの味と風味を最大化するために、5つの因子（A:カカオの割合、B:砂糖の種類、C:ミルクの量、D:ナッツの有無、E:香料の種類）を選び、それぞれ3つのレベルで実験を行うことにしました。ABとBCには交互作用がありそうです。ボブはL₂₇(3¹³)直行表を使用して、効率的に実験を進めます。

【1】直交表の割り付け
　以下のように割り付けを行った。

【2】実験結果
　実験結果を以下に示す。

【3】各要因の平方和、平均平方和、F₀を計算
計算式は以下の通り。計算例として因子A、因子AB、誤差eのみ記載しますが、他の因子についても同様に計算します。

【4】分散分析表を作成

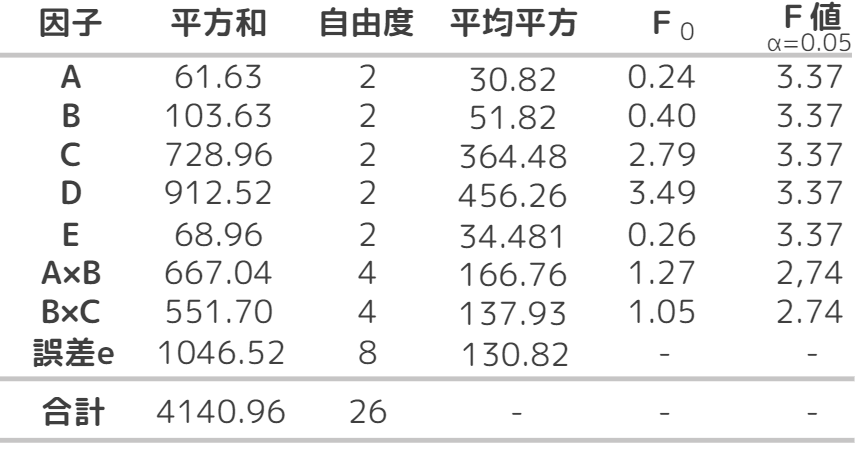
【結論】
この分散分析結果から、F値＜F₀である因子D（ミルクの量）が影響力のある因子であることがわかります。それ以外の因子ははF値＞F0であることから影響が少ないことが示されています。ただし、因子C（ナッツの有無）は比較的F₀が大きいので検討を要する因子だと考えられます。

これにより、万人受けするおいしいチョコレートを作りにはミルクの量が重要であると結論づけられます。

エクセルを使ったF値の求め方
直交表を使う場合はエクセルを使う場合が多いと思います。F値はエクセルの関数で求めることができます。関数は”=F.INV.RT(α, 因子の自由度, 合計の自由度)”です。上記の例（因子A）では”=F.INV.RT(0.05, 2, 26)”となります。