実験計画法｜2水準直交表を例題で解説（交互作用ありの場合）

実験計画法とは、「多数の実験条件の組み合わせを総当たりまたは一部の組み合わせで実験を行い、最適な条件を効率よく見つける手法」です。

水準の組み合わせを総当たりで行う実験を要因配置実験（二元配置分散分析など）、一部の水準の組み合わせを行う実験を部分配置実験（直交表など）といいます。

この記事では部分配置実験に分類される”2水準の直交表（交互作用がある場合）”について解説します。

2水準直交表｜L8(27)の因子割り付け方法（交互作用がある場合）

交互作用が”ない場合”と”ある場合”では直交表への割り付け方が異なります。交互作用がある場合は、どの列に交互作用が出るかを考えて割り付けを行う必要があります。ここでは交互作用がある場合の割り付け方をL₈(2⁷)を使って解説します。

L₈(2⁷)の名称の意味や直交表の見方については”交互作用なしの場合”で説明しています。
また、3水準の場合は”3水準直交表（交互作用ありの場合）”で解説しています。

割り付け方法１｜交互作用表を使う

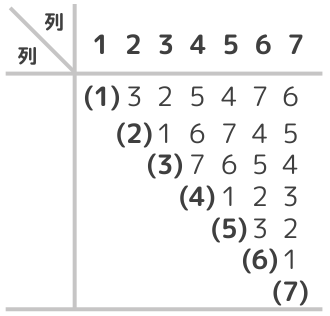
一つ目は直交表に付属している交互作用表を使う方法です。この表の見方は、例えば”2列目”と”6列目”との交互作用を求めるときは、”2行目の6列目”の数字を確認します。この場合は”4”になるので、2列目と6列目の交互作用は4列目に出ることがわかります。

割り付け方法２｜直交表の成分記号を使う

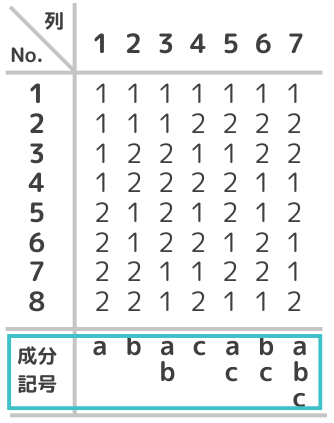
二つ目は直交表の成分記号欄を使う方法です。成分記号を使っても交互作用の列を求めることができます。
成分記号欄を使う場合は、以下ルールに従います。

• 交互作用の出る列は、各列の成分記号の積を持つ列
• 掛け算で得られた成分記号の2乗は”1”とする（a²=b²=c²=1)

たとえば、1列目（成分記号：a）と2列目（成分記号：ｂ）の交互作用は3列目（成分記号：ab）。2列目（成分記号：ｂ）と6列目（成分記号：ｂｃ）の交互作用は4列目（b×bc=b²c=1×c=c）。

割り付け方法３｜線点図を使う

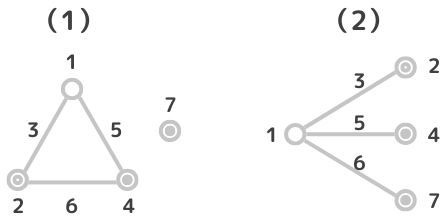
3つ目は線点図を使う方法です。線点図の数字は列番号を表します。2つの点を結ぶ線は交互作用を表しています。
たとえば、左図（1）は”点1”と”点2”を結ぶ線に”3”とあるので、1列目と2列目の交互作用は3列目に出ることがわかります。

【例】交互作用ありのL8(27)の実施手順

交互作用ありのL₈(2⁷)を使った実験を具体例で解説します。

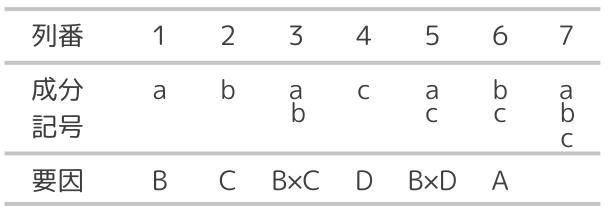
【1】直交表の割り付け
　以下のように割り付けを行った。

【2】各要因の平方和、F₀を計算

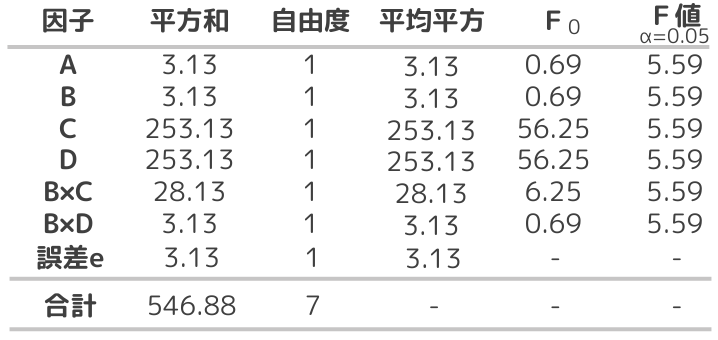
【3】分散分析表を作成

【結論】
この分散分析結果から、F値＜F₀である因子C（卵の数）、因子D（焼く温度）が影響力のある因子であることがわかります。因子A（粉の種類）、因子B（牛乳の量）、B×C、B×Dの交互作用はF値＞F0であることから影響が少ないことが示されています。

これにより、完璧なパンケーキを作るには、卵の数、焼く温度が重要であると結論づけられます。